Finding Area Of Irregular Figures Worksheets
News Co
Apr 05, 2025 · 6 min read
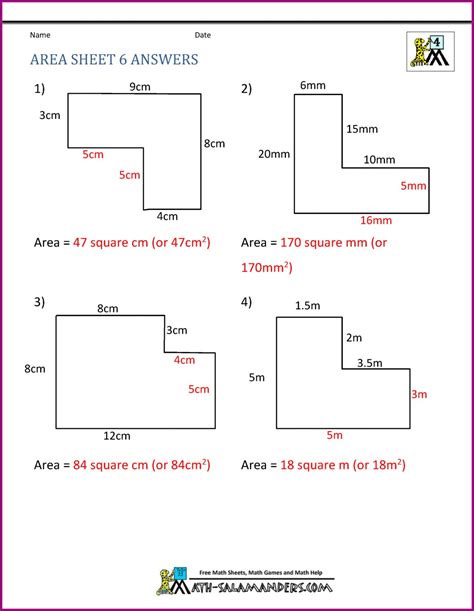
Table of Contents
Finding the Area of Irregular Figures: Worksheets and Strategies for Success
Finding the area of regular shapes like squares, rectangles, and circles is straightforward. However, calculating the area of irregular figures presents a unique challenge, requiring a blend of geometrical understanding and strategic problem-solving. This comprehensive guide delves into various methods for determining the area of irregular figures, providing you with the tools and knowledge to tackle worksheets and real-world applications with confidence. We'll explore diverse approaches, emphasizing practical application and building a strong foundational understanding. We'll also discuss how to approach worksheets effectively and improve your problem-solving skills.
Understanding Irregular Figures
Before diving into calculation methods, it's crucial to define what constitutes an irregular figure. Simply put, an irregular figure is any shape that doesn't fit neatly into the standard geometrical categories. These shapes lack consistent, easily measurable sides or angles. Examples include oddly shaped plots of land, irregularly shaped pools, or complex designs in artwork. Their unpredictability demands more sophisticated approaches than simply applying a standard formula.
Methods for Finding the Area of Irregular Figures
Several effective methods can be used to approximate or accurately determine the area of irregular figures. The best approach depends on the specific shape and the tools available.
1. Grid Method (or Square Counting)
This is a fundamental approach, especially useful for beginners. It involves overlaying a grid of squares (e.g., graph paper) onto the irregular figure.
- Procedure: Count the number of whole squares completely within the figure. Then, estimate the area of the partial squares by visually judging their fractions (e.g., a half-square counts as 0.5). Sum the whole squares and the estimated partial square areas to obtain an approximate total area.
- Advantages: Simple and visually intuitive; requires minimal mathematical knowledge.
- Disadvantages: Accuracy depends heavily on the grid size and the estimator's judgment. Smaller grid squares improve accuracy but require more counting. It's not suitable for extremely complex figures.
Example: Imagine an irregular blob on graph paper. You count 15 whole squares completely inside the blob and estimate that the partial squares add up to approximately 7.5 squares. Therefore, the estimated area is 15 + 7.5 = 22.5 square units.
2. Decomposition Method (Breaking Down into Regular Shapes)
This method involves dissecting the irregular figure into smaller, recognizable shapes like triangles, rectangles, or trapezoids. This allows you to calculate the area of each component shape and then sum them up for the total area.
- Procedure: Carefully draw lines to partition the irregular figure into familiar shapes. Calculate the area of each individual shape using the appropriate formula (e.g., area of a triangle = 0.5 * base * height). Add up all the individual areas to get the total area of the irregular figure.
- Advantages: Relatively accurate, especially with precisely drawn partitions; good for figures with clear, definable segments.
- Disadvantages: Requires good geometrical intuition and accurate measurements; not ideal for figures with highly irregular boundaries.
Example: An irregular polygon could be broken into several triangles. If you calculate the area of each triangle and add them, you'll get the total area of the original polygon.
3. Using a Planimeter
A planimeter is a mechanical or digital instrument used to measure the area of a plane surface. It's particularly useful for precisely measuring irregularly shaped areas on maps or drawings.
- Procedure: Trace the outline of the irregular figure with the planimeter's tracer. The instrument directly provides the area measurement.
- Advantages: Highly accurate for physical drawings or maps.
- Disadvantages: Requires specialized equipment. Not easily accessible for general use.
4. The Trapezoidal Rule (Numerical Integration)
This is a more advanced method, ideal for irregularly shaped figures represented by a graph or a set of data points. It approximates the area under a curve by dividing the area into a series of trapezoids.
- Procedure: Divide the area into a series of narrow trapezoids. Calculate the area of each trapezoid using the formula (0.5 * (base1 + base2) * height). Sum the individual trapezoidal areas to obtain an approximation of the total area. The smaller the trapezoids, the greater the accuracy.
- Advantages: Highly accurate for figures with smooth, curved boundaries; suitable for data-driven analysis.
- Disadvantages: Requires understanding of calculus concepts; can be computationally intensive for many trapezoids.
5. Using Computer Software
Various software packages (e.g., CAD software, image processing software) can be employed to determine the area of irregular figures. These programs often utilize algorithms that efficiently approximate or precisely calculate area based on digital representations of the shape.
- Procedure: Input the figure's coordinates or scan/import an image. The software will provide the calculated area.
- Advantages: High accuracy and efficiency, especially for complex figures.
- Disadvantages: Requires access to and familiarity with specialized software.
Practical Application: Working with Worksheets
Irregular figures worksheets offer invaluable practice in applying these methods. To successfully tackle these worksheets:
- Read the instructions carefully: Understand the specific requirements and the methods suggested.
- Draw diagrams: Creating clear, labeled diagrams helps visualize the problem and guides your approach. For decomposition, sketch your dividing lines clearly.
- Show your work: Document your steps, calculations, and reasoning. This makes it easier to identify errors and demonstrate your understanding.
- Use appropriate units: Always include the correct units (e.g., square centimeters, square meters) in your answers.
- Check your answers: Review your work to ensure accuracy and logical consistency. Compare your results with a solution key if available.
- Practice regularly: The more you practice, the better you'll become at choosing the optimal method and performing the calculations efficiently.
Types of Irregular Figures Found on Worksheets
Worksheets often present a variety of irregular figures, challenging you to apply different strategies. These include:
- Irregular polygons: Polygons with sides of unequal length and angles that are not necessarily 90 degrees.
- Freeform shapes: Shapes with completely irregular, curved boundaries.
- Composite figures: Shapes formed by combining multiple regular and irregular shapes.
- Figures represented by coordinates: Shapes defined by a set of points, requiring you to use coordinate geometry techniques.
- Shapes derived from real-world scenarios: Worksheets often use diagrams of plots of land, building plans, or other practical applications.
Developing Strong Problem-Solving Skills
Beyond mastering the calculation methods, the key to success with irregular figure area problems lies in developing robust problem-solving skills.
- Spatial Reasoning: Practice visualizing shapes in different ways. The ability to mentally manipulate and decompose a figure is invaluable.
- Geometric Knowledge: A strong foundation in geometry is essential. Familiarize yourself with formulas for areas of regular shapes (triangles, rectangles, trapezoids, circles).
- Measurement Skills: Accurate measurement is crucial, especially when using methods like decomposition or grid counting.
- Estimation: Practice estimating areas visually. This is important for the grid method and for checking the reasonableness of your answers.
- Pattern Recognition: Identify patterns and relationships between figures. This can help you choose the most efficient method.
Advanced Concepts and Challenges
As you progress, you might encounter more complex scenarios, including:
- Calculating areas using calculus: This involves using integration techniques to find the area under curves.
- Working with three-dimensional shapes: Extending the principles of area calculation to find surface areas of irregular three-dimensional objects.
- Handling irregularly shaped figures with holes: Subtracting the area of the hole from the total area.
Conclusion
Mastering the calculation of the area of irregular figures is a journey that enhances your geometrical understanding and sharpens your problem-solving abilities. By understanding and practicing the various methods, including grid counting, decomposition, planimetry, the trapezoidal rule, and the utilization of software, you'll confidently tackle worksheets and real-world applications. Remember that consistent practice, a strong foundation in geometry, and honed problem-solving skills are the cornerstones of success in this area of mathematics. Tackle those worksheets with enthusiasm and watch your skills grow!
Latest Posts
Related Post
Thank you for visiting our website which covers about Finding Area Of Irregular Figures Worksheets . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.