Finding Area Under A Curve Calculator
News Co
Apr 06, 2025 · 6 min read
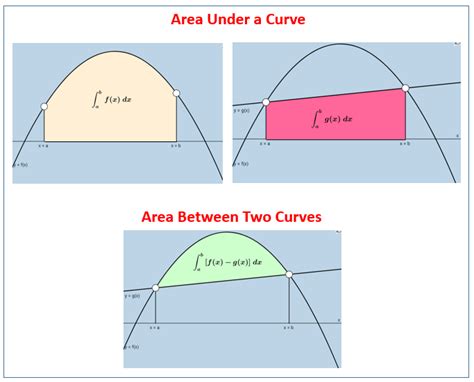
Table of Contents
Finding the Area Under a Curve Calculator: A Comprehensive Guide
Finding the area under a curve is a fundamental concept in calculus with wide-ranging applications in various fields, from physics and engineering to economics and statistics. Manually calculating this area can be complex and time-consuming, especially for intricate functions. This is where a finding the area under a curve calculator proves invaluable. This comprehensive guide explores the concept, its applications, different methods of calculation, and the advantages of using online calculators.
Understanding the Area Under a Curve
The area under a curve represents the integral of a function over a specified interval. Visually, imagine the area enclosed between the curve, the x-axis, and two vertical lines representing the limits of integration. This area quantifies the cumulative effect or magnitude of the function over that interval.
Why is it important?
The significance of finding this area stems from its ability to model real-world phenomena. For example:
- Physics: Calculating the distance traveled by an object given its velocity function over time.
- Engineering: Determining the work done by a force over a specific displacement.
- Economics: Calculating the total revenue generated by a company over a given period, given its revenue function.
- Statistics: Finding the probability of an event occurring within a certain range, given its probability density function.
Methods for Calculating the Area Under a Curve
Several methods exist for calculating the area under a curve, each with its own strengths and limitations:
1. Analytical Integration (Exact Method)
This is the most accurate method, involving finding the indefinite integral of the function and then evaluating it at the limits of integration using the Fundamental Theorem of Calculus. This yields the exact area. However, it requires a good understanding of integration techniques and is not always feasible for complex functions. For example, finding the integral of f(x) = e^(-x²), which is crucial in statistics, cannot be expressed using elementary functions.
2. Numerical Integration (Approximate Method)
When analytical integration is impractical, numerical methods provide approximate solutions. These methods divide the area under the curve into smaller segments and approximate the area of each segment. The sum of these smaller areas approximates the total area. Common numerical integration techniques include:
- Riemann Sums: This is a basic method that approximates the area using rectangles. It can be further divided into left Riemann sum, right Riemann sum, and midpoint Riemann sum. The accuracy increases as the number of rectangles increases.
- Trapezoidal Rule: This method uses trapezoids instead of rectangles to approximate the area, generally providing a more accurate approximation than Riemann sums with the same number of subdivisions.
- Simpson's Rule: This method uses parabolas to approximate the curve, offering even greater accuracy than the trapezoidal rule. It requires an even number of intervals.
These numerical methods are readily implemented in a finding the area under a curve calculator. The calculator will perform the calculations based on the chosen method and the specified number of intervals.
3. Monte Carlo Method (Random Sampling)
This probabilistic method involves randomly sampling points within a defined region containing the area under the curve. By determining the ratio of points falling under the curve to the total number of points, an estimate of the area can be obtained. This method is particularly useful for complex shapes and high-dimensional integrals. However, it requires a large number of samples to achieve a reasonable level of accuracy.
The Advantages of Using a Finding the Area Under a Curve Calculator
Using an online calculator for finding the area under a curve offers several significant advantages:
- Ease of Use: Calculators provide a user-friendly interface, simplifying the process, even for complex functions. You simply input the function and integration limits, and the calculator handles the calculations.
- Speed and Efficiency: Calculators perform calculations much faster than manual methods, especially for numerical integration techniques requiring multiple iterations.
- Accuracy: Calculators, especially those employing advanced numerical methods, offer high accuracy, particularly when dealing with complex functions where analytical solutions are unavailable.
- Reduced Error: Manual calculations are prone to human error. Calculators minimize these errors, ensuring reliable results.
- Visualization: Many calculators provide graphical representations of the function and the calculated area, enhancing understanding and visualization.
- Accessibility: Online calculators are readily accessible from anywhere with an internet connection, eliminating the need for specialized software or tools.
Choosing the Right Finding the Area Under a Curve Calculator
When selecting a calculator, consider the following features:
- Supported Functions: Ensure the calculator supports the types of functions you need to integrate (e.g., polynomials, trigonometric functions, exponential functions).
- Integration Methods: Check the available integration methods (analytical, Riemann sums, trapezoidal rule, Simpson's rule, etc.). More sophisticated methods generally provide better accuracy.
- Accuracy: Look for calculators that offer adjustable precision or specify the error bounds of their approximations.
- User Interface: Choose a calculator with an intuitive and user-friendly interface.
- Visualization Capabilities: The ability to visualize the function and calculated area can significantly improve understanding.
- Additional Features: Some calculators may offer additional features like step-by-step solutions, handling of improper integrals, or support for multiple variables.
Applications in Different Fields
The application of finding the area under a curve extends to numerous fields:
1. Physics:
- Displacement Calculation: Integrating a velocity function over time gives the total displacement of an object.
- Work Calculation: Integrating a force function over distance gives the total work done.
- Fluid Dynamics: Calculating the flow rate of a fluid through a pipe, given its velocity profile.
2. Engineering:
- Stress and Strain Analysis: Integrating stress or strain distributions provides valuable information about the structural integrity of materials.
- Signal Processing: Determining the average power of a signal.
- Heat Transfer: Calculating the total heat transferred between two surfaces.
3. Economics:
- Consumer Surplus and Producer Surplus: These economic concepts are directly related to the area under a demand or supply curve.
- Total Revenue Calculation: Integrating a revenue function over time gives the total revenue generated.
4. Statistics and Probability:
- Probability Density Function: The probability of a random variable falling within a specific range is the area under its probability density function over that range.
- Statistical Inference: Numerous statistical tests rely on calculating areas under probability distributions.
Conclusion
Finding the area under a curve is a powerful tool with wide-ranging applications across diverse fields. While analytical integration provides exact results when feasible, numerical methods, readily implemented in online calculators, offer efficient and accurate approximations for complex functions. Using a finding the area under a curve calculator simplifies the process, reduces errors, and allows for a better understanding of the concepts and applications. By understanding the different methods and selecting the right calculator, you can unlock the power of integration for your specific needs. Remember to consider the features offered by different calculators to ensure you choose the most suitable one for your task. The ability to quickly and accurately calculate these areas opens doors to a deeper understanding of numerous complex systems and phenomena.
Latest Posts
Related Post
Thank you for visiting our website which covers about Finding Area Under A Curve Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.