Fractions That Are Equivalent To 2/3
News Co
Apr 06, 2025 · 5 min read
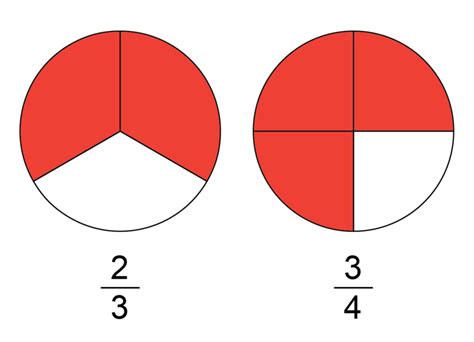
Table of Contents
Fractions Equivalent to 2/3: A Comprehensive Guide
Understanding equivalent fractions is a fundamental concept in mathematics. This article delves deep into the world of fractions equivalent to 2/3, exploring various methods to find them, their applications, and the importance of mastering this skill. We'll move beyond simple multiplication and delve into the conceptual understanding that underlies this crucial mathematical concept.
What are Equivalent Fractions?
Equivalent fractions represent the same portion of a whole, even though they look different. They have the same value but are expressed using different numerators and denominators. For instance, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. Each fraction represents exactly half of a whole. The key to understanding equivalent fractions lies in the concept of proportional relationships.
Finding Fractions Equivalent to 2/3: The Multiplication Method
The most straightforward method for finding equivalent fractions is through multiplication. To obtain an equivalent fraction to 2/3, you multiply both the numerator (2) and the denominator (3) by the same non-zero integer. This ensures that the ratio between the numerator and the denominator remains constant, preserving the value of the fraction.
Examples:
- Multiplying by 2: (2 x 2) / (3 x 2) = 4/6
- Multiplying by 3: (2 x 3) / (3 x 3) = 6/9
- Multiplying by 4: (2 x 4) / (3 x 4) = 8/12
- Multiplying by 5: (2 x 5) / (3 x 5) = 10/15
- Multiplying by 10: (2 x 10) / (3 x 10) = 20/30
This method generates an infinite number of equivalent fractions for 2/3, each representing the same portion of a whole. The larger the multiplier, the larger the numbers in the equivalent fraction.
Finding Fractions Equivalent to 2/3: The Division Method (Simplifying Fractions)
While multiplication creates equivalent fractions with larger numbers, division simplifies fractions to their lowest terms. If you're given a fraction and need to determine if it's equivalent to 2/3, you can simplify it by dividing both the numerator and denominator by their greatest common divisor (GCD). If the simplified fraction is 2/3, then the original fraction is equivalent.
Example:
Let's consider the fraction 12/18. The GCD of 12 and 18 is 6. Dividing both the numerator and denominator by 6, we get:
12 ÷ 6 / 18 ÷ 6 = 2/3
Therefore, 12/18 is an equivalent fraction to 2/3. This method is crucial for determining equivalency and simplifying complex fractions.
Visualizing Equivalent Fractions
Visual aids can significantly enhance understanding. Imagine a circle divided into three equal parts. Shading two of these parts represents 2/3. Now, imagine dividing each of those three parts into two smaller equal parts. You now have six parts, and four of them are shaded, representing 4/6. This visual representation clearly demonstrates the equivalence of 2/3 and 4/6. The same principle applies to other divisions, creating visual proofs for numerous equivalent fractions.
The Importance of Understanding Equivalent Fractions
The ability to identify and work with equivalent fractions is paramount in various mathematical contexts:
- Simplifying Fractions: Reducing fractions to their simplest form improves clarity and eases calculations.
- Adding and Subtracting Fractions: Before adding or subtracting fractions, you need to find a common denominator – often an equivalent fraction of one of the original fractions.
- Comparing Fractions: Determining which fraction is larger or smaller requires expressing them with a common denominator.
- Solving Equations: Working with fractions in equations necessitates understanding equivalent fractions for manipulation and simplification.
- Real-World Applications: Equivalent fractions have practical applications in various fields, from cooking and construction to finance and data analysis. For example, understanding proportions and ratios for scaling recipes or building structures relies heavily on this concept.
Beyond the Basics: Exploring Patterns and Relationships
As we've seen, there are infinitely many fractions equivalent to 2/3. However, understanding the underlying patterns can help predict and generate these equivalents systematically. The key lies in the consistent ratio between the numerator and the denominator. Every equivalent fraction is a multiple of 2/3. This means that you can express any equivalent fraction as (2n) / (3n), where 'n' represents any positive integer. This formula provides a powerful tool for generating and verifying equivalent fractions.
Advanced Concepts and Applications:
The understanding of equivalent fractions lays the foundation for more complex mathematical concepts:
- Ratios and Proportions: Equivalent fractions are directly related to ratios and proportions. They represent the same relationship between two quantities.
- Decimal and Percentage Conversions: Equivalent fractions can be easily converted to decimals and percentages, expanding their applications in various real-world scenarios. For example, 2/3 is approximately equal to 0.667 or 66.7%.
- Algebraic Expressions: The concept of equivalent fractions extends to algebraic expressions, where equivalent expressions represent the same value but are written differently.
Troubleshooting Common Mistakes:
A common mistake is incorrectly multiplying or dividing only the numerator or denominator. Remember, you must always perform the same operation on both the numerator and the denominator to maintain the value of the fraction.
Another common issue arises when simplifying fractions. Students might not find the greatest common divisor, leading to an incomplete simplification. Mastering the process of finding the GCD is crucial for accurate simplification.
Practice Makes Perfect:
The best way to master equivalent fractions is through consistent practice. Start with simple exercises and gradually increase the difficulty. Use visual aids and real-world examples to reinforce your understanding. Practice identifying equivalent fractions, simplifying fractions, and applying the concept in various problem-solving scenarios.
Conclusion:
Understanding equivalent fractions is a fundamental mathematical skill with wide-ranging applications. This article explored various methods for finding fractions equivalent to 2/3, including multiplication and division, and highlighted the importance of this concept in simplifying fractions, adding and subtracting fractions, and solving equations. By mastering this fundamental concept, students build a strong foundation for more advanced mathematical topics and real-world applications. Consistent practice and a focus on understanding the underlying principles are essential for achieving proficiency in this area. Remember, the ability to confidently identify and work with equivalent fractions is a key stepping stone to success in higher-level mathematics.
Latest Posts
Latest Posts
-
Ratio Word Problems Worksheets With Answers
Apr 07, 2025
-
What Is The Square Root Of 4096
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Fractions That Are Equivalent To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
