Gcf Of 16 32 And 40
News Co
May 08, 2025 · 5 min read
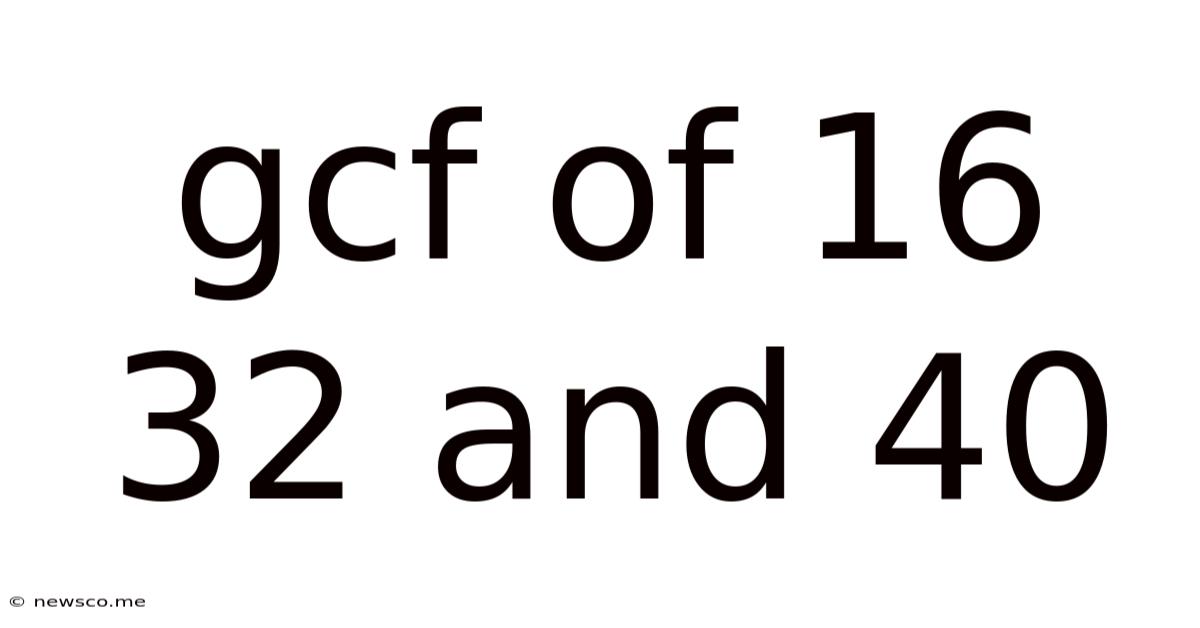
Table of Contents
Finding the Greatest Common Factor (GCF) of 16, 32, and 40: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will delve into the process of determining the GCF of 16, 32, and 40, exploring multiple methods and providing a deeper understanding of the underlying principles. We'll also touch upon the broader significance of GCFs and their practical uses.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. It represents the largest shared factor among the given numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Why is finding the GCF important?
The ability to find the GCF is crucial for several mathematical operations:
- Simplifying Fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. Dividing both by the GCF gives the equivalent fraction in its lowest terms.
- Algebraic Simplification: GCFs are essential in simplifying algebraic expressions, often used to factor polynomials and solve equations.
- Problem Solving: Many real-world problems involving ratios, proportions, and groupings require finding the GCF for efficient solutions.
Methods for Finding the GCF of 16, 32, and 40
There are several effective methods for finding the GCF of a set of numbers. Let's explore the most common approaches, applying them to find the GCF of 16, 32, and 40.
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 32: 1, 2, 4, 8, 16, 32
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the lists, we see that the common factors are 1, 2, 4, and 8. The greatest of these common factors is 8. Therefore, the GCF of 16, 32, and 40 is 8.
This method is straightforward for smaller numbers but can become cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2<sup>4</sup>
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2<sup>3</sup> x 5
The only common prime factor is 2. The lowest power of 2 among the factorizations is 2<sup>3</sup>, which equals 8. Therefore, the GCF of 16, 32, and 40 is 8.
3. Euclidean Algorithm Method
The Euclidean algorithm is an efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by repeatedly applying the algorithm. Let's find the GCF of 16, 32, and 40 using this method.
First, we find the GCF of 16 and 32:
- Divide 32 by 16: 32 ÷ 16 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF of 16 and 32 is 16.
Next, we find the GCF of 16 and 40:
- Divide 40 by 16: 40 ÷ 16 = 2 with a remainder of 8.
- Divide 16 by 8: 16 ÷ 8 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF of 16 and 40 is 8.
Therefore, the GCF of 16, 32, and 40 is 8.
Applications of GCF in Real-World Scenarios
The concept of GCF extends beyond abstract mathematical problems. It finds practical applications in various fields:
- Baking: When preparing recipes that call for specific ratios of ingredients, finding the GCF allows bakers to scale recipes up or down while maintaining the correct proportions.
- Construction: In construction projects, determining the optimal dimensions for tiles or bricks often involves finding the GCF to ensure efficient and aesthetically pleasing layouts.
- Gardening: When arranging plants in rows or grids, using the GCF helps create uniform and well-organized gardens.
- Data Organization: In computer science and data analysis, the GCF can aid in optimizing data storage and processing by finding common factors in data structures.
Advanced Concepts and Extensions
While the GCF is typically applied to integers, the concept can be extended to other mathematical objects, such as polynomials. Finding the GCF of polynomials involves identifying the common factors among the polynomial terms. This process is crucial in simplifying algebraic expressions and solving polynomial equations.
Conclusion: Mastering the GCF
Understanding and efficiently calculating the greatest common factor is a fundamental skill with far-reaching applications. Whether employing the listing factors method, prime factorization, or the Euclidean algorithm, mastering these techniques provides a valuable tool for various mathematical and real-world problems. The methods described in this guide offer different approaches depending on the complexity of the numbers involved, enabling you to choose the most suitable strategy for each situation. Remember, a solid grasp of the GCF will significantly improve your problem-solving abilities and deepen your understanding of mathematical principles. The example of finding the GCF of 16, 32, and 40 serves as a clear illustration of these methods and their applicability.
Latest Posts
Related Post
Thank you for visiting our website which covers about Gcf Of 16 32 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.