Gcf Of 35 56 And 63
News Co
Apr 03, 2025 · 6 min read
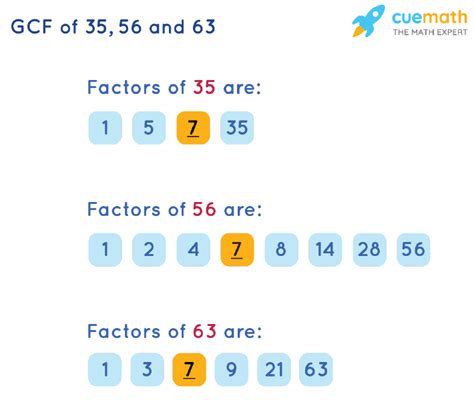
Table of Contents
Finding the Greatest Common Factor (GCF) of 35, 56, and 63: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article will delve into the process of determining the GCF of 35, 56, and 63, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader context of GCF and its significance in various mathematical fields.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into all the numbers in the set. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Understanding the GCF is crucial for several mathematical operations:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For instance, the fraction 12/18 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving Algebraic Equations: GCF plays a vital role in factoring algebraic expressions, a key step in solving many equations.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for many advanced theorems and algorithms.
-
Real-world Applications: The concept extends to practical applications such as dividing resources evenly, determining the size of the largest square tile that can perfectly cover a rectangular area, and many other scenarios involving proportionality and divisibility.
Methods for Finding the GCF of 35, 56, and 63
We will explore several methods to find the GCF of 35, 56, and 63:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to all three.
- Factors of 35: 1, 5, 7, 35
- Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
- Factors of 63: 1, 3, 7, 9, 21, 63
Comparing the lists, we can see that the only common factor among 35, 56, and 63 is 7. Therefore, the GCF of 35, 56, and 63 is 7. This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime Factorization of 35: 5 x 7
- Prime Factorization of 56: 2 x 2 x 2 x 7 = 2³ x 7
- Prime Factorization of 63: 3 x 3 x 7 = 3² x 7
The common prime factor among all three numbers is 7. Since 7 appears only once in each factorization, the lowest power is 7¹. Therefore, the GCF of 35, 56, and 63 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by repeatedly applying the algorithm. Here's how it works:
-
Find the GCF of the first two numbers (35 and 56):
- Divide the larger number (56) by the smaller number (35): 56 ÷ 35 = 1 with a remainder of 21.
- Replace the larger number with the smaller number (35) and the smaller number with the remainder (21).
- Repeat: 35 ÷ 21 = 1 with a remainder of 14.
- Repeat: 21 ÷ 14 = 1 with a remainder of 7.
- Repeat: 14 ÷ 7 = 2 with a remainder of 0.
- The GCF of 35 and 56 is the last non-zero remainder, which is 7.
-
Find the GCF of the result (7) and the third number (63):
- Divide the larger number (63) by the smaller number (7): 63 ÷ 7 = 9 with a remainder of 0.
- The GCF of 7 and 63 is 7.
Therefore, the GCF of 35, 56, and 63 is 7. The Euclidean algorithm is particularly efficient for larger numbers because it avoids the need to find all the factors.
Applications of GCF in Different Contexts
The GCF has a wide range of applications beyond simply simplifying fractions:
1. Simplifying Ratios and Proportions
GCF is essential in simplifying ratios and proportions to their simplest forms. This is crucial in various fields, including chemistry (mixing solutions), cooking (scaling recipes), and engineering (designing structures).
2. Geometric Problems
GCF is used to solve geometric problems involving area and dimensions. For example, finding the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the length and width of the floor.
3. Number Theory and Cryptography
GCF is a cornerstone of number theory and has significant applications in cryptography, particularly in RSA encryption, where the security relies heavily on the difficulty of finding the GCF of very large numbers.
4. Modular Arithmetic
GCF is fundamental in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). This is used in various areas, including computer science and cryptography.
5. Data Analysis and Statistics
While not directly involved in calculations, understanding the concept of common factors and divisibility can be helpful in data analysis and statistics when dealing with frequency distributions and data grouping.
Advanced Concepts Related to GCF
For a deeper understanding, let's explore some related advanced concepts:
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of all the numbers in a set. The GCF and LCM are related by the formula: GCF(a, b) x LCM(a, b) = a x b. This relationship can be extended to more than two numbers.
-
Coprime Numbers: Two numbers are considered coprime (or relatively prime) if their GCF is 1. This property is crucial in number theory and cryptography.
-
Extended Euclidean Algorithm: This is an extension of the Euclidean algorithm that, in addition to finding the GCF, also finds integers x and y such that ax + by = GCF(a, b). This has applications in solving linear Diophantine equations.
Conclusion
Finding the GCF of 35, 56, and 63, as demonstrated through multiple methods, showcases the importance of this fundamental mathematical concept. Understanding the GCF is crucial for a wide array of mathematical operations and real-world applications. Whether using the listing factors method, prime factorization, or the efficient Euclidean algorithm, the ability to determine the GCF is an essential skill for anyone pursuing further studies in mathematics or related fields. The connections between GCF, LCM, coprime numbers, and the extended Euclidean algorithm highlight the rich interconnectedness of mathematical concepts and the far-reaching impact of seemingly simple ideas. The applications within number theory and cryptography demonstrate the power of fundamental concepts to underpin complex systems and secure technologies.
Latest Posts
Related Post
Thank you for visiting our website which covers about Gcf Of 35 56 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.