Gcf Of 42 126 And 210
News Co
Mar 26, 2025 · 5 min read
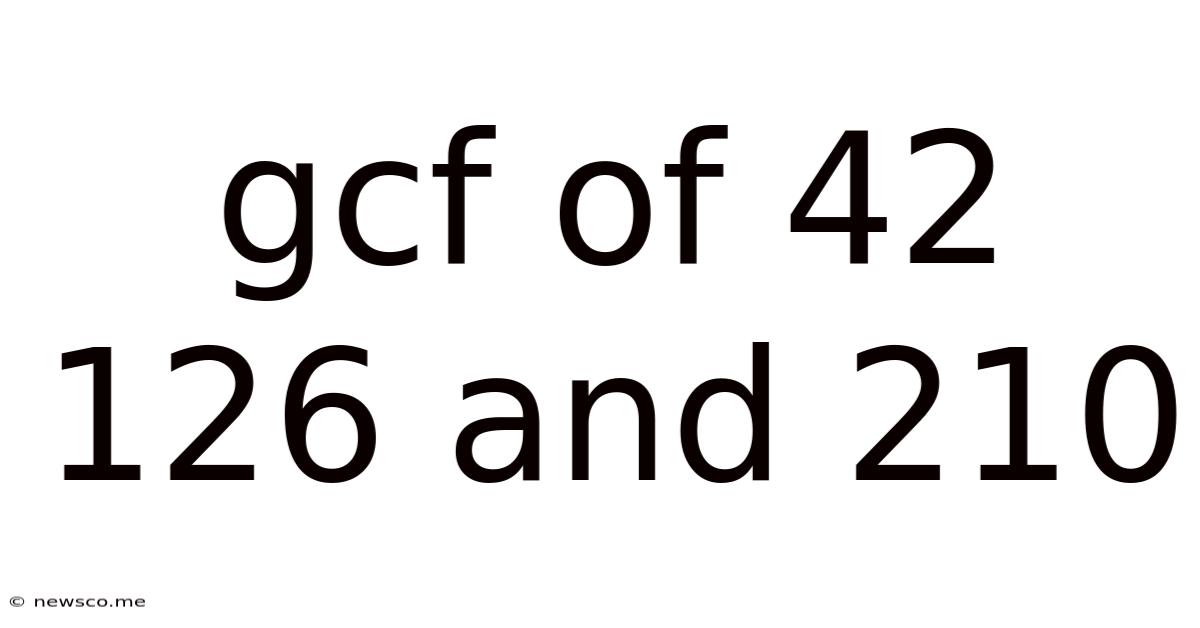
Table of Contents
Finding the Greatest Common Factor (GCF) of 42, 126, and 210: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications across various fields. This comprehensive guide will walk you through multiple methods for determining the GCF of 42, 126, and 210, explaining the underlying principles and providing practical examples. We'll explore the prime factorization method, the Euclidean algorithm, and the listing factors method, highlighting the strengths and weaknesses of each approach.
Understanding the Greatest Common Factor (GCF)
Before diving into the methods, let's clarify what the GCF represents. The GCF of a set of numbers is the largest number that divides each of the numbers in the set without leaving a remainder. In simpler terms, it's the biggest number that goes into all the given numbers evenly. Understanding this definition is crucial for selecting and applying the appropriate method to find the GCF.
Method 1: Prime Factorization
The prime factorization method is a robust and widely used technique for finding the GCF. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. The GCF is then determined by identifying the common prime factors and multiplying them together.
Steps:
-
Find the prime factorization of each number:
- 42 = 2 x 3 x 7
- 126 = 2 x 3² x 7
- 210 = 2 x 3 x 5 x 7
-
Identify the common prime factors: Notice that 2, 3, and 7 are common to all three factorizations.
-
Multiply the common prime factors: The GCF is the product of these common factors: 2 x 3 x 7 = 42
Therefore, the GCF of 42, 126, and 210 is 42.
Advantages of Prime Factorization:
- Conceptual clarity: This method directly demonstrates the underlying principle of the GCF.
- Works for any number of integers: It's easily adaptable to finding the GCF of more than three numbers.
Disadvantages of Prime Factorization:
- Can be time-consuming for large numbers: Finding the prime factorization of very large numbers can be computationally intensive.
- Requires knowledge of prime numbers: A good understanding of prime numbers is necessary to effectively apply this method.
Method 2: Listing Factors
The listing factors method involves systematically listing all the factors of each number and then identifying the largest common factor. This method is straightforward but can be less efficient for larger numbers with many factors.
Steps:
-
List the factors of each number:
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
- Factors of 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126
- Factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
-
Identify the common factors: Compare the lists and find the factors that appear in all three lists. These are the common factors.
-
Find the greatest common factor: The largest number among the common factors is the GCF. In this case, the largest common factor is 42.
Therefore, the GCF of 42, 126, and 210 is 42.
Advantages of Listing Factors:
- Simple and intuitive: Easy to understand and apply, particularly for smaller numbers.
Disadvantages of Listing Factors:
- Inefficient for larger numbers: Listing all factors becomes cumbersome and time-consuming for larger numbers with many factors.
- Prone to errors: Manually listing factors increases the chance of missing factors or making mistakes.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. For more than two numbers, we apply the algorithm iteratively.
Steps:
-
Find the GCF of 42 and 126:
- 126 = 42 x 3 + 0. Since the remainder is 0, the GCF(42, 126) = 42.
-
Find the GCF of the result (42) and the next number (210):
- 210 = 42 x 5 + 0. Since the remainder is 0, the GCF(42, 210) = 42.
Therefore, the GCF of 42, 126, and 210 is 42.
Advantages of the Euclidean Algorithm:
- Efficient for larger numbers: Significantly more efficient than the listing factors method for large numbers.
- Systematic and less prone to errors: The algorithmic nature reduces the chances of human error.
Disadvantages of the Euclidean Algorithm:
- Less intuitive: The underlying mathematical principle might not be as immediately obvious as in the prime factorization method.
Choosing the Right Method
The best method for finding the GCF depends on the specific numbers involved and your comfort level with different mathematical techniques.
- Small numbers with easily identifiable factors: The listing factors method is suitable.
- Larger numbers or numbers with many factors: The Euclidean algorithm is the most efficient.
- Understanding the underlying principles: The prime factorization method provides valuable insight into the nature of GCFs.
Applications of GCF
The GCF has numerous applications in various areas of mathematics and beyond:
- Simplifying fractions: Finding the GCF allows you to simplify fractions to their lowest terms.
- Solving word problems: Many word problems involving sharing or dividing quantities equally rely on the concept of the GCF.
- Geometry: The GCF is used in geometry problems involving finding the dimensions of objects with a common measure.
- Computer science: The Euclidean algorithm, used for finding the GCF, has applications in cryptography and other areas of computer science.
Conclusion
Determining the greatest common factor is a crucial skill in mathematics. This guide has explored three distinct methods – prime factorization, listing factors, and the Euclidean algorithm – each with its own advantages and disadvantages. Choosing the most appropriate method depends on the context and the numbers involved. By understanding these methods and their applications, you'll be well-equipped to tackle GCF problems efficiently and confidently. Remember to practice regularly to reinforce your understanding and improve your speed and accuracy. Mastering the GCF is not just about finding a numerical answer; it's about developing a deeper understanding of fundamental mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about Gcf Of 42 126 And 210 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.