Given Ac Bd Prove Ab Cd
News Co
Apr 23, 2025 · 5 min read
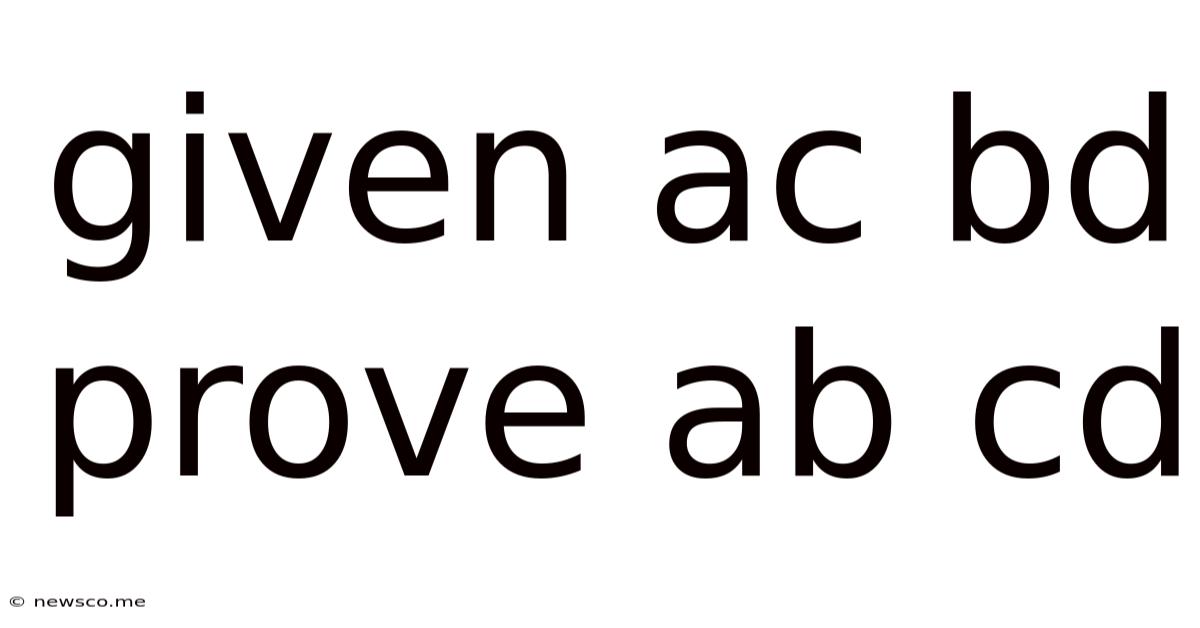
Table of Contents
Given AC = BD, Prove AB = CD: A Comprehensive Exploration of Geometric Proofs
This article delves into the fascinating world of geometric proofs, specifically addressing the challenge of proving AB = CD given that AC = BD. While the statement itself, without additional context or constraints, is not universally true, we'll explore various scenarios where it could be true, examining the necessary conditions and providing rigorous mathematical demonstrations. We’ll cover different approaches, including utilizing congruent triangles, vector methods, and coordinate geometry. This comprehensive analysis will equip you with a deeper understanding of geometric reasoning and proof techniques.
Understanding the Problem's Ambiguity
The statement "Given AC = BD, prove AB = CD" is inherently ambiguous. Without specifying the geometric context—the shape involved, the relationships between points A, B, C, and D—it's impossible to provide a universally valid proof. The lengths AC and BD could belong to completely different geometric figures, making the assertion false.
To make the problem solvable, we need to introduce additional information or constraints. Let's consider several scenarios where a proof might be possible:
Scenario 1: Parallelogram with Equal Diagonals
Theorem: In a parallelogram with equal diagonals, opposite sides are equal.
Let's assume ABCD is a parallelogram, and we are given that AC = BD. We want to prove that AB = CD (and consequently, BC = AD).
Proof:
-
Diagonals bisect each other: In any parallelogram, the diagonals bisect each other. This means that the point of intersection, let's call it O, divides AC and BD into two equal segments: AO = OC = BO = OD.
-
Given AC = BD: This is our initial condition.
-
Transitive Property: Since AO = OC and BO = OD, and AC = BD, we can deduce that AO = BO = OC = OD.
-
Congruent Triangles: Consider triangles ΔABO and ΔCDO. We have:
- AO = OD (from step 3)
- BO = OC (from step 3)
- ∠AOB = ∠COD (vertically opposite angles are equal)
-
Side-Angle-Side (SAS) Congruence: By the SAS congruence criterion, ΔABO ≅ ΔCDO.
-
Corresponding Sides are Equal: Because corresponding parts of congruent triangles are equal, we have AB = CD.
Therefore, in a parallelogram with equal diagonals, opposite sides are indeed equal.
Scenario 2: Specific Quadrilaterals
Theorem: Under certain conditions in specific quadrilaterals (e.g., isosceles trapezoids, certain kites), the equality of diagonals can imply the equality of specific sides.
Let's consider an isosceles trapezoid ABCD, where AB || CD. If we are given that AC = BD, we can attempt to prove AB = CD. However, this requires further exploration and a different proof strategy. The proof would involve constructing perpendiculars from A and B to CD, creating congruent right-angled triangles, and using properties of isosceles trapezoids. This is more complex and depends heavily on the specific properties of the isosceles trapezoid. It would not be a general proof applicable to all quadrilaterals.
A similar approach can be applied to certain types of kites where a specific configuration of angles and diagonals might lead to the equality of certain sides given the equality of diagonals.
Scenario 3: Using Vector Methods
Vector methods offer a powerful and elegant approach to solving geometric problems.
Let's represent the points A, B, C, and D as vectors a, b, c, and d, respectively.
-
Given AC = BD: This translates to c - a = d - b.
-
Rearranging: We can rearrange the equation to c + b = d + a.
However, this equation alone doesn't directly imply AB = CD (b - a = d - c). We need additional information or constraints on the vectors to prove the equality of AB and CD. For instance, if we knew that the vectors formed a parallelogram (b - a = c - d) or a rhombus, the equality would follow from the vector representation of the geometric conditions.
This demonstrates that simply knowing the equality of the vector representations of AC and BD is insufficient without further constraints.
Scenario 4: Coordinate Geometry
Using coordinate geometry, we can assign coordinates to points A, B, C, and D. Let's say:
- A = (x₁, y₁)
- B = (x₂, y₂)
- C = (x₃, y₃)
- D = (x₄, y₄)
Then AC = √((x₃ - x₁)² + (y₃ - y₁)²) and BD = √((x₄ - x₂)² + (y₄ - y₂)²)
Given that AC = BD, we have:
√((x₃ - x₁)² + (y₃ - y₁)²) = √((x₄ - x₂)² + (y₄ - y₂)²)
Squaring both sides:
(x₃ - x₁)² + (y₃ - y₁)² = (x₄ - x₂)² + (y₄ - y₂)²
Again, this equation alone doesn't directly imply that AB = CD. The equation describes the relationship between the distances, but it doesn't explicitly state the equality of AB and CD. We would need more information, such as the specific coordinates or a relationship between them defining a particular geometric shape (e.g., a parallelogram, a rhombus, etc.).
Conclusion: The Importance of Context
This detailed analysis highlights the crucial role of context in geometric proofs. The initial statement, "Given AC = BD, prove AB = CD," is insufficient to establish a general proof. The equality holds true under specific conditions and within certain geometric shapes, such as parallelograms with equal diagonals. However, without specifying the geometric context or adding constraints, the assertion is not universally true.
This exploration showcases the importance of careful consideration of problem statements and the need for precise definitions and constraints when working with geometric proofs. The various approaches presented—using congruent triangles, vectors, and coordinate geometry—demonstrate the versatility of mathematical techniques in addressing geometric challenges. The ambiguity of the initial statement serves as a valuable lesson in the precise and rigorous nature of mathematical reasoning.
Latest Posts
Related Post
Thank you for visiting our website which covers about Given Ac Bd Prove Ab Cd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.