Given That Abc Def Solve For X
News Co
May 08, 2025 · 4 min read
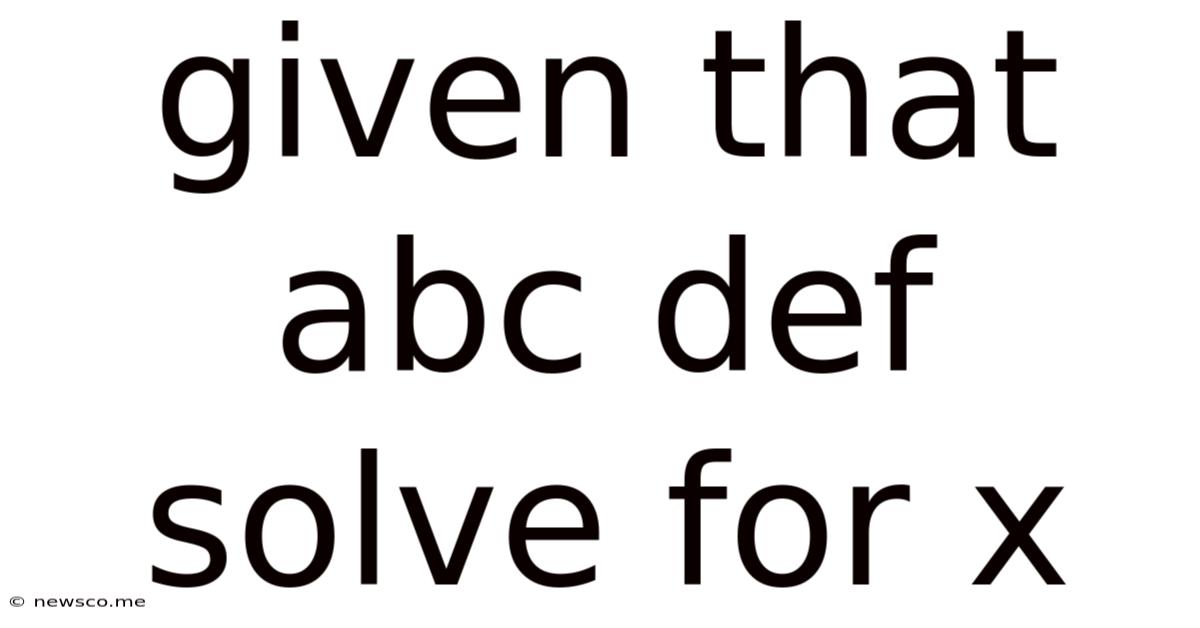
Table of Contents
Decoding the Enigma: Solving for 'x' in the Equation ABC DEF
The seemingly simple equation "ABC DEF solve for x" presents a fascinating challenge. At first glance, it appears incomplete and ambiguous. However, by delving deeper into the potential interpretations and applying various mathematical principles, we can explore multiple solutions and uncover the underlying logic. This article will dissect this enigmatic equation, offering various approaches to solving for 'x' depending on how we interpret the given symbols.
Understanding the Ambiguity: Interpreting ABC and DEF
The core issue lies in interpreting "ABC" and "DEF". Are these:
- Variables: Representing unknown numerical values?
- Numbers in a different base: Perhaps a base-other-than-10 system (e.g., base-16, hexadecimal)?
- Representations of functions or operations: Indicating specific mathematical operations to be performed?
- Part of a larger, hidden equation: A snippet from a more complex mathematical expression?
The lack of explicit operators between ABC and DEF further complicates matters. Are we dealing with addition, subtraction, multiplication, division, or a more intricate combination? The possibilities are extensive, highlighting the crucial need for clear problem definition in mathematics.
Scenario 1: ABC and DEF as Variables
If we assume ABC and DEF represent variables, the equation becomes essentially unsolvable without further information. We have two unknowns and no equation connecting them to 'x'. To solve for 'x', we would need at least one additional equation relating ABC, DEF, and x. For example:
- Example 1: If ABC + DEF = x, then we cannot solve for x without knowing the values of ABC and DEF.
- Example 2: If ABC * DEF = x, again, we're stuck without numerical values for ABC and DEF.
This scenario highlights the importance of well-defined problems in algebra. A complete algebraic equation requires a sufficient number of equations (or constraints) to match the number of unknowns. Without this, the problem becomes underdetermined, meaning there are infinitely many possible solutions.
Scenario 2: ABC and DEF as Numbers in a Different Base
Let's explore the possibility of ABC and DEF representing numbers in a different numerical base. The most common alternative base is hexadecimal (base-16), using the digits 0-9 and A-F (A=10, B=11, C=12, D=13, E=14, F=15).
If we assume base-16:
- ABC (base-16) = 1016² + 1116¹ + 12*16⁰ = 2560 + 176 + 12 = 2748 (base-10)
- DEF (base-16) = 1316² + 1416¹ + 15*16⁰ = 3328 + 224 + 15 = 3567 (base-10)
Even with these base-10 conversions, we still need an operator and an equation involving 'x' to solve for it. For instance:
- If 2748 + 3567 = x, then x = 6315
- If 2748 * 3567 = x, then x = 9791716
- If 2748 / 3567 = x, then x ≈ 0.77
This base conversion approach necessitates a clear specification of the intended base and a defined relationship between ABC, DEF, and x.
Scenario 3: ABC and DEF as Functions or Operations
A more abstract interpretation involves viewing ABC and DEF as representing mathematical functions or operations. This would require significantly more context and details to even begin solving for 'x'. The equation might represent a system of equations, a transformation, or a complex algorithm.
For example, ABC could signify a function: f(x) = Ax² + Bx + C and DEF could be another function: g(x) = Dx² + Ex + F. Solving for x would then depend on the relationship between f(x) and g(x).
Scenario 4: Part of a Larger Equation
The presented snippet "ABC DEF solve for x" could be a fragment of a larger, more comprehensive mathematical expression. In this case, the context surrounding this fragment is crucial. Without the full equation, any attempt to solve for 'x' is mere speculation.
Advanced Considerations: Solving Systems of Equations
If we were presented with additional equations involving ABC, DEF, and x, we could employ various techniques to solve for x. These techniques might include:
- Substitution: Express one variable in terms of others and substitute it into other equations.
- Elimination: Combine equations to eliminate one or more variables, simplifying the system.
- Matrix methods: For systems of linear equations, matrix algebra can provide elegant and efficient solutions.
- Numerical methods: For complex or non-linear equations, iterative numerical methods (e.g., Newton-Raphson method) could be employed to find approximate solutions.
Conclusion: The Importance of Precision in Mathematical Notation
The ambiguity inherent in the equation "ABC DEF solve for x" emphasizes the critical role of precise mathematical notation. Without clear definitions of the symbols (ABC, DEF, and their relationship to 'x') and the operators connecting them, the problem remains fundamentally unsolvable.
To obtain a meaningful solution, one needs to specify:
- The meaning of ABC and DEF: Are they variables, numbers in a specific base, functions, or something else?
- The relationship between ABC, DEF, and x: What operations connect these elements?
- The full context of the equation: Is this a complete equation, or a fragment of a larger problem?
By providing this crucial context, the seemingly simple task of "solving for x" becomes achievable. This analysis highlights not only the importance of problem definition but also the versatility and richness of mathematical approaches to problem-solving. The exploration of different interpretations demonstrates the multiple perspectives and solutions that can arise from even the most compact mathematical statements.
Latest Posts
Latest Posts
-
How Many 40 Hour Weeks In A Year
May 08, 2025
-
Are All Isosceles Right Triangles Similar
May 08, 2025
-
850 En Ingles Como Se Escribe
May 08, 2025
-
80 Dollars With 40 Percent Off
May 08, 2025
-
Enter The Degree Of The Polynomial Below
May 08, 2025
Related Post
Thank you for visiting our website which covers about Given That Abc Def Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.