Graph Of X 2 2x 2
News Co
Apr 15, 2025 · 5 min read
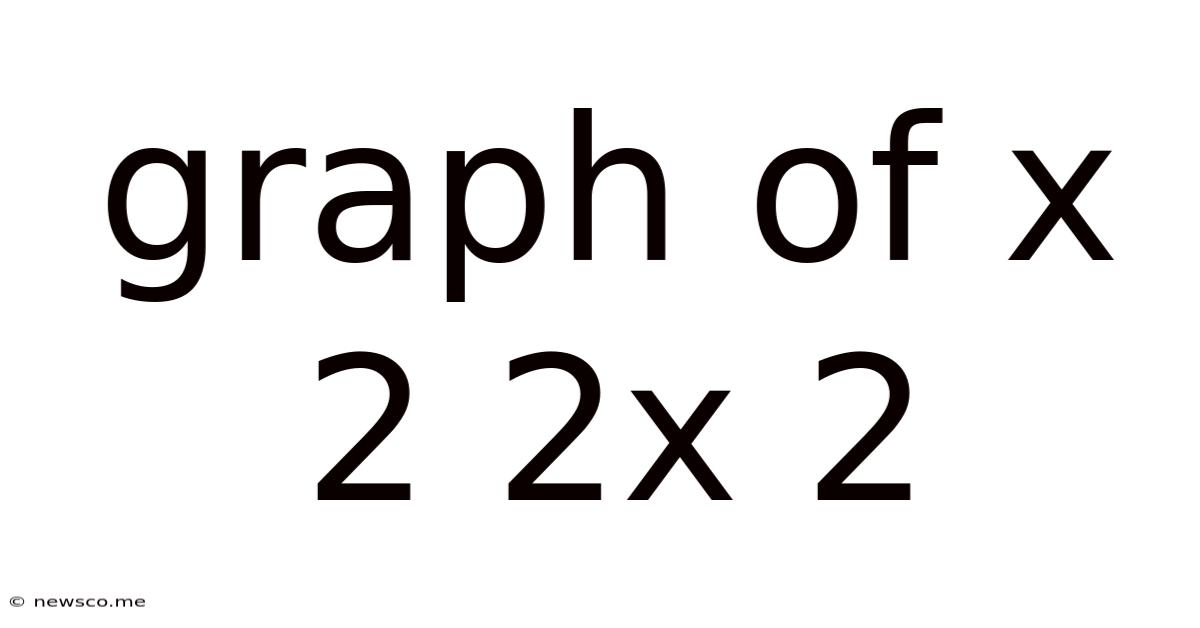
Table of Contents
Exploring the Graph of x² + 2x - 2: A Comprehensive Analysis
The quadratic equation x² + 2x - 2 represents a parabola, a fundamental curve in mathematics with widespread applications in various fields, from physics and engineering to economics and computer science. Understanding its graph involves analyzing key features such as its vertex, intercepts, axis of symmetry, and concavity. This article provides a thorough exploration of these features and offers insights into how to effectively represent this quadratic function graphically.
Understanding the Quadratic Equation
Before diving into the graphical representation, let's first analyze the equation itself: x² + 2x - 2 = 0. This is a standard quadratic equation in the form ax² + bx + c = 0, where a = 1, b = 2, and c = -2. The coefficient 'a' determines the parabola's concavity (whether it opens upwards or downwards), 'b' influences the parabola's horizontal shift, and 'c' represents the y-intercept.
Determining the Concavity
Since a = 1 (a positive value), the parabola opens upwards. This means the vertex represents the minimum point on the graph. If 'a' were negative, the parabola would open downwards, and the vertex would represent the maximum point.
Finding the Vertex
The vertex of a parabola is its turning point. For a quadratic equation in the form ax² + bx + c, the x-coordinate of the vertex is given by: x = -b / 2a. In our case:
x = -2 / (2 * 1) = -1
To find the y-coordinate, we substitute this x-value back into the original equation:
y = (-1)² + 2(-1) - 2 = -3
Therefore, the vertex of the parabola is (-1, -3).
Identifying the x-intercepts (Roots)
The x-intercepts, also known as roots or zeros, are the points where the parabola intersects the x-axis (where y = 0). To find these points, we solve the quadratic equation:
x² + 2x - 2 = 0
This equation doesn't factor easily, so we'll use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values:
x = [-2 ± √(2² - 4 * 1 * -2)] / (2 * 1) x = [-2 ± √(12)] / 2 x = [-2 ± 2√3] / 2 x = -1 ± √3
Therefore, the x-intercepts are approximately -2.732 and 0.732.
Determining the y-intercept
The y-intercept is the point where the parabola intersects the y-axis (where x = 0). To find this, we simply substitute x = 0 into the equation:
y = (0)² + 2(0) - 2 = -2
Therefore, the y-intercept is (0, -2).
Axis of Symmetry
The axis of symmetry is a vertical line that divides the parabola into two symmetrical halves. It passes through the vertex. The equation of the axis of symmetry is given by:
x = -b / 2a
In our case, this is x = -1.
Sketching the Graph
Now that we have all the key features – the vertex, x-intercepts, y-intercept, and axis of symmetry – we can accurately sketch the graph of x² + 2x - 2. The parabola opens upwards, with its vertex at (-1, -3). The x-intercepts are approximately -2.732 and 0.732, and the y-intercept is at (0, -2). The axis of symmetry is the vertical line x = -1.
Remember to plot these points on a coordinate plane and draw a smooth, U-shaped curve connecting them. This curve represents the graph of the quadratic equation.
Advanced Analysis and Applications
This seemingly simple quadratic equation holds a wealth of further analytical possibilities and practical applications.
Completing the Square
Completing the square transforms the quadratic equation into vertex form, providing another way to find the vertex and understand the parabola's behavior:
x² + 2x - 2 = (x² + 2x + 1) - 1 - 2 = (x + 1)² - 3
This vertex form, y = (x + 1)² - 3, clearly shows the vertex at (-1, -3).
Calculus Applications
Calculus provides tools to explore more sophisticated aspects of the graph:
- Derivatives: The first derivative, 2x + 2, gives the slope of the tangent line at any point on the parabola. Setting it to zero gives the x-coordinate of the vertex (-1).
- Integrals: The definite integral of the function over a given interval represents the area under the curve within that interval. This is useful in numerous applications, such as calculating the area of a parabolic reflector or determining the displacement of an object under parabolic motion.
Real-World Applications
Quadratic functions, and hence their graphs, are vital in modelling various real-world phenomena:
- Projectile Motion: The trajectory of a projectile under gravity follows a parabolic path. The equation can be used to determine the maximum height, range, and flight time.
- Optimization Problems: Finding the maximum or minimum values of a quadratic function is fundamental in optimization problems in engineering and business, such as maximizing profit or minimizing cost.
- Engineering Design: Parabolic curves are used in the design of bridges, antennas, and reflectors due to their unique reflective properties.
Software and Tools for Graphing
Numerous software tools and online calculators can assist in graphing quadratic equations and other functions. These tools often provide interactive features, allowing users to manipulate parameters and observe the resulting changes in the graph. Exploring these tools can enhance understanding and provide a visual representation to complement the analytical approach.
Conclusion
The graph of x² + 2x - 2 represents a parabola with a vertex at (-1, -3), x-intercepts at approximately -2.732 and 0.732, a y-intercept at (0, -2), and an axis of symmetry at x = -1. Understanding its features through both algebraic manipulation and graphical representation is crucial in grasping its mathematical significance and appreciating its wide range of applications in various fields. The depth of analysis possible, from basic intercepts to calculus-based insights, underscores the rich mathematical tapestry woven within this seemingly simple quadratic equation. By utilizing various methods and tools, one can gain a comprehensive understanding of this fundamental function and its impact on numerous real-world scenarios. Further exploration into its applications in diverse fields will only deepen one's appreciation for the power and versatility of quadratic equations.
Latest Posts
Related Post
Thank you for visiting our website which covers about Graph Of X 2 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.