Greatest Common Factor Of 56 And 84
News Co
Apr 07, 2025 · 5 min read
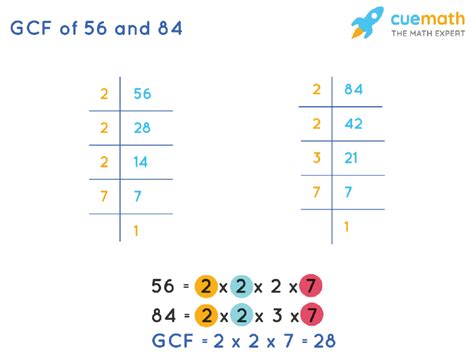
Table of Contents
Finding the Greatest Common Factor (GCF) of 56 and 84: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic equations. This comprehensive guide will delve into various methods for determining the GCF of 56 and 84, explaining each step in detail and providing practical examples to solidify your understanding. We'll also explore the broader context of GCFs and their importance in various mathematical fields.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of the numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
This concept is crucial in simplifying fractions, finding equivalent ratios, and solving various algebraic problems. Mastering the techniques for finding the GCF is an essential skill for anyone studying mathematics.
Method 1: Listing Factors
The most straightforward method for finding the GCF is by listing all the factors of each number and identifying the largest common factor.
Finding the Factors of 56:
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28, and 56.
Finding the Factors of 84:
The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, and 84.
Identifying the Common Factors:
Now, let's compare the two lists and identify the common factors: 1, 2, 4, 7, 14, and 28.
Determining the Greatest Common Factor:
The largest number among the common factors is 28. Therefore, the GCF of 56 and 84 is 28.
This method is simple for smaller numbers, but it can become cumbersome and time-consuming when dealing with larger numbers with many factors.
Method 2: Prime Factorization
Prime factorization is a more efficient method for finding the GCF, especially when dealing with larger numbers. It involves expressing each number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Prime Factorization of 56:
56 = 2 x 28 = 2 x 2 x 14 = 2 x 2 x 2 x 7 = 2³ x 7¹
Prime Factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3¹ x 7¹
Identifying Common Prime Factors:
Now, we identify the common prime factors in both factorizations: 2 and 7.
Calculating the GCF:
To find the GCF, we multiply the common prime factors raised to the lowest power present in either factorization:
GCF(56, 84) = 2² x 7¹ = 4 x 7 = 28
This method is more efficient than listing factors, especially for larger numbers. It provides a structured approach that minimizes the chance of overlooking common factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Applying the Euclidean Algorithm to 56 and 84:
- Step 1: Start with the larger number (84) and the smaller number (56).
- Step 2: Subtract the smaller number from the larger number: 84 - 56 = 28.
- Step 3: Replace the larger number with the result (28) and repeat the process using the previous smaller number (56) as the new larger number. So, we now have 56 and 28.
- Step 4: Subtract the smaller number from the larger number: 56 - 28 = 28.
- Step 5: Since both numbers are now equal (28 and 28), the GCF is 28.
The Euclidean algorithm offers a systematic approach that's particularly advantageous when dealing with large numbers, as it significantly reduces the computational effort compared to other methods.
Applications of the Greatest Common Factor
Understanding and calculating the GCF has numerous applications across various mathematical disciplines and real-world scenarios:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 56/84 can be simplified by dividing both the numerator and denominator by their GCF (28), resulting in the equivalent fraction 2/3.
-
Solving Algebraic Equations: The GCF is used in factoring algebraic expressions, which is crucial for solving equations and simplifying complex algebraic problems.
-
Ratio and Proportion Problems: GCF helps in simplifying ratios to their simplest form, making it easier to understand and compare proportions.
-
Geometry: In geometry, the GCF plays a role in problems involving scaling and similar figures.
-
Number Theory: GCF is a fundamental concept in number theory, used extensively in various advanced mathematical theorems and proofs.
Conclusion
Finding the greatest common factor is a vital skill in mathematics with broad applications. We've explored three different methods: listing factors, prime factorization, and the Euclidean algorithm. While listing factors is suitable for small numbers, prime factorization and the Euclidean algorithm provide more efficient solutions for larger numbers. Understanding these methods equips you with the tools to tackle various mathematical problems involving GCF, simplifying fractions, solving equations, and much more. Choosing the appropriate method depends on the complexity of the numbers involved and your comfort level with each approach. Regardless of the method used, mastering the concept of GCF is a cornerstone of mathematical proficiency. Practice regularly to enhance your understanding and speed in calculating the GCF of any given pair of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 56 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.