Half Of 1 1/4 In Fraction
News Co
Apr 26, 2025 · 4 min read
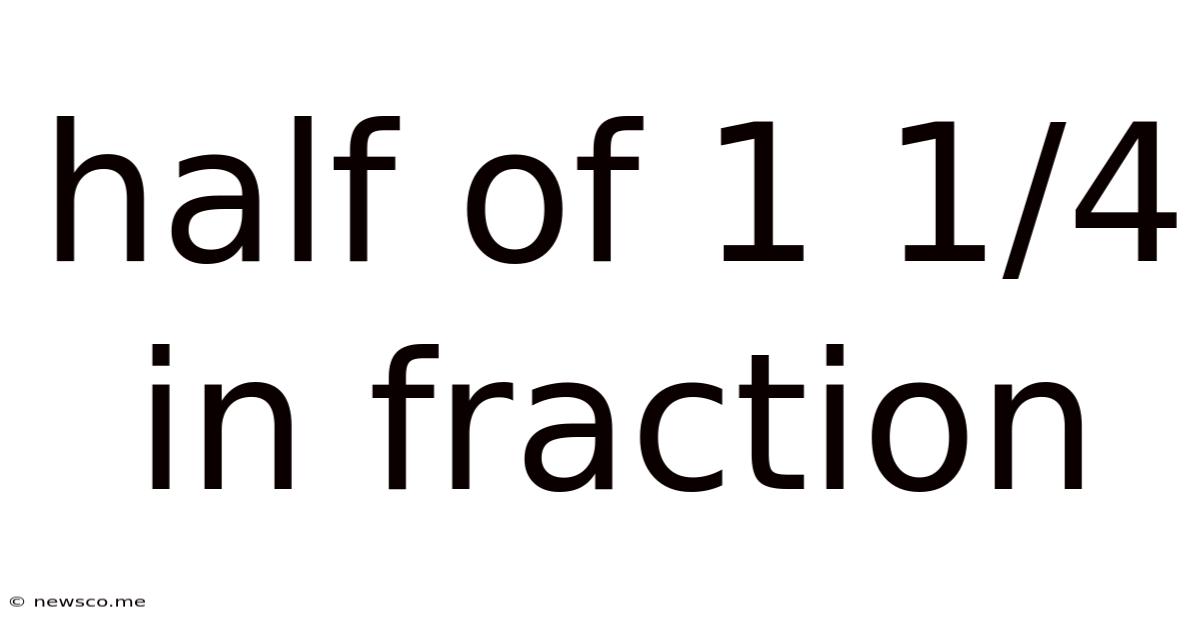
Table of Contents
Half of 1 1/4: A Deep Dive into Fraction Division
Finding half of any number is a fundamental mathematical operation, and understanding how to do this with fractions is crucial for mastering more complex mathematical concepts. This comprehensive guide will explore how to calculate half of 1 1/4, providing a step-by-step explanation, tackling common misconceptions, and expanding on the broader implications of fractional division. We'll cover various approaches, ensuring you grasp the core principles and can apply them to similar problems confidently.
Understanding the Problem: Half of 1 1/4
The question, "What is half of 1 1/4?" translates mathematically to finding ½ of 1 ¼. This involves dividing a mixed number (1 ¼) by 2. While it might seem daunting at first, breaking down the problem into smaller, manageable steps simplifies the process significantly.
Converting Mixed Numbers to Improper Fractions
Before diving into the division, it's best to convert the mixed number 1 ¼ into an improper fraction. This makes the calculation much cleaner and less error-prone. To do this, we follow these steps:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator: 4 + 1 = 5
- Keep the same denominator: The denominator remains 4.
Therefore, 1 ¼ is equivalent to the improper fraction 5/4.
Calculating Half: The Division Process
Now that we've converted 1 ¼ to 5/4, we can proceed with the division: (5/4) / 2. There are two primary ways to approach this division:
Method 1: Multiplying by the Reciprocal
This method involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply flipping the numerator and the denominator. The reciprocal of 2 (which can be written as 2/1) is 1/2.
Therefore, the calculation becomes:
(5/4) * (1/2) = (5 * 1) / (4 * 2) = 5/8
Thus, half of 1 1/4 is 5/8.
Method 2: Dividing the Numerator
Another approach involves directly dividing the numerator of the improper fraction by the whole number. In this case, we divide 5 by 2:
5 / 2 = 2.5
Then, we keep the same denominator:
2.5/4
This is a valid result, but it's often preferable to express the answer as a simple fraction. To convert 2.5/4 to a fraction, we can multiply both the numerator and denominator by 2 to get rid of the decimal:
(2.5 * 2) / (4 * 2) = 5/8
Again, we arrive at the answer: 5/8.
Visualizing the Solution
Understanding fractions can be easier when you visualize them. Imagine a pizza cut into four slices. 1 ¼ pizzas represents five slices (one whole pizza plus one quarter). Half of that is 2 ½ slices, which is 5/8 of a whole pizza. This visual representation confirms our mathematical calculation.
Expanding on Fractional Division: More Examples
Let's apply the principles we've learned to a few more examples to solidify your understanding of fractional division.
Example 1: Half of 2 1/3
- Convert to an improper fraction: 2 1/3 = (2 * 3 + 1) / 3 = 7/3
- Divide by 2 (multiply by 1/2): (7/3) * (1/2) = 7/6
- Simplify (if necessary): 7/6 can be expressed as 1 1/6.
Therefore, half of 2 1/3 is 7/6 or 1 1/6.
Example 2: One-third of 1 ½
- Convert to an improper fraction: 1 ½ = (1 * 2 + 1) / 2 = 3/2
- Divide by 3 (multiply by 1/3): (3/2) * (1/3) = 3/6
- Simplify: 3/6 simplifies to 1/2
Therefore, one-third of 1 ½ is 1/2.
Common Mistakes to Avoid
Several common mistakes can arise when dealing with fractions:
-
Incorrect Conversion to Improper Fractions: Carefully follow the steps for converting mixed numbers to improper fractions. A simple mistake here will propagate through the entire calculation.
-
Errors in Reciprocal Multiplication: Remember to flip the numerator and denominator when finding the reciprocal.
-
Forgetting to Simplify: Always simplify your final answer to its lowest terms.
-
Incorrect Order of Operations: When dealing with multiple operations (like addition, subtraction, multiplication, and division), ensure you follow the correct order of operations (PEMDAS/BODMAS).
Beyond the Basics: Applications of Fractional Division
Understanding fractional division is crucial in various real-life situations and advanced mathematical concepts:
-
Cooking and Baking: Recipes often involve fractional amounts of ingredients. Calculating half a recipe requires fractional division.
-
Construction and Engineering: Accurate measurements are critical, and understanding fractions helps in precise calculations.
-
Finance: Calculating percentages, interest rates, and proportions often involves working with fractions.
-
Data Analysis and Statistics: Many statistical calculations rely on understanding and manipulating fractions.
Conclusion: Mastering Fractions for Mathematical Success
Mastering fractional division, as demonstrated by calculating half of 1 1/4, is a foundational skill for success in mathematics and various practical applications. By consistently applying the correct methods, carefully converting mixed numbers, and diligently simplifying results, you can confidently tackle similar problems and build a strong foundation for more advanced mathematical concepts. Remember to practice regularly and visualize the problems to enhance your understanding. The more you work with fractions, the more intuitive and effortless these calculations will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Half Of 1 1/4 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.