Highest Common Factor Of 24 And 32
News Co
Apr 06, 2025 · 5 min read
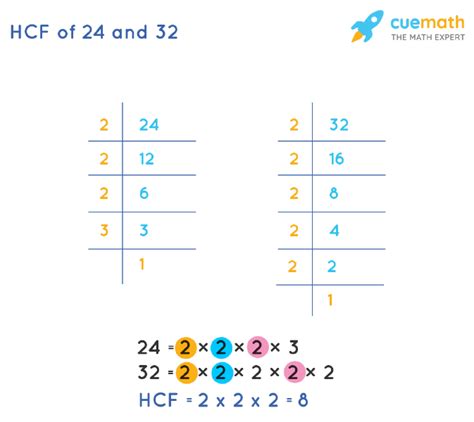
Table of Contents
Highest Common Factor (HCF) of 24 and 32: A Deep Dive
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields. This article delves into the HCF of 24 and 32, exploring different methods to determine it and highlighting its significance in number theory and beyond. We'll move beyond a simple answer and explore the underlying principles, providing a comprehensive understanding of this mathematical concept.
Understanding Highest Common Factor (HCF)
The highest common factor (HCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding HCF is crucial for simplifying fractions, solving algebraic equations, and even in more advanced areas like cryptography.
For instance, let's consider the factors of 24 and 32:
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 32: 1, 2, 4, 8, 16, 32
By comparing the lists, we can identify the common factors: 1, 2, 4, and 8. The highest among these common factors is 8. Therefore, the HCF of 24 and 32 is 8.
Methods for Finding the HCF
Several methods exist to efficiently determine the HCF of two numbers. Let's explore some of the most common and effective approaches:
1. Listing Factors Method
This is the most straightforward method, particularly useful for smaller numbers. As demonstrated above, we list all the factors of each number and identify the largest common factor. However, this method becomes less practical for larger numbers as the number of factors increases significantly.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Let's apply this to 24 and 32:
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
To find the HCF, we identify the common prime factors and take the lowest power of each. In this case, the only common prime factor is 2, and the lowest power is 2³. Therefore, the HCF is 2³ = 8. This method is efficient even for larger numbers, although finding the prime factorization can be time-consuming for very large numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially for larger ones. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to 24 and 32:
- 32 - 24 = 8
- 24 - 8 = 16
- 16 - 8 = 8
- 8 - 8 = 0
The process stops when the remainder is 0. The last non-zero remainder is the HCF, which is 8.
The Euclidean algorithm can be expressed more concisely using modulo operation:
- 32 mod 24 = 8
- 24 mod 8 = 0
Again, the HCF is 8. This algorithm is significantly more efficient than listing factors or prime factorization for larger numbers because it reduces the size of the numbers at each step.
Applications of HCF
The HCF finds applications in diverse areas:
1. Simplifying Fractions
The HCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their HCF. For example, to simplify the fraction 24/32, we divide both the numerator and the denominator by their HCF, which is 8:
24/32 = (24 ÷ 8) / (32 ÷ 8) = 3/4
2. Solving Word Problems
Many word problems involving division or sharing require finding the HCF. For example, consider a problem where you need to divide 24 apples and 32 oranges into identical groups without any leftovers. The HCF (8) represents the maximum number of identical groups you can create. Each group would contain 3 apples (24/8) and 4 oranges (32/8).
3. Number Theory
The HCF plays a fundamental role in number theory. It's used in concepts like modular arithmetic, coprime numbers (numbers with an HCF of 1), and solving Diophantine equations (equations involving integers).
4. Cryptography
HCF and related concepts like the Euclidean algorithm are essential in public-key cryptography, which is used to secure online communications. Algorithms like RSA rely on the difficulty of finding the prime factorization of large numbers, which is directly related to finding the HCF.
Beyond the Basics: Exploring Related Concepts
Understanding the HCF opens doors to more advanced mathematical concepts:
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest positive integer that is divisible by both numbers. The HCF and LCM are related by the formula: HCF(a, b) x LCM(a, b) = a x b. For 24 and 32, the LCM is 96.
-
Coprime Numbers: Two numbers are coprime (or relatively prime) if their HCF is 1. For example, 15 and 28 are coprime because their HCF is 1.
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. The HCF plays a role in determining properties and relationships within modular arithmetic systems.
Conclusion: The Enduring Importance of HCF
The seemingly simple concept of the highest common factor extends far beyond basic arithmetic. Its applications in fraction simplification, word problem solving, number theory, and cryptography highlight its enduring importance in mathematics and its impact on various fields. Mastering the different methods for finding the HCF – listing factors, prime factorization, and the efficient Euclidean algorithm – equips you with a powerful tool for tackling a wide range of mathematical problems and understanding more complex mathematical structures. The HCF of 24 and 32, while seemingly a straightforward calculation, serves as a gateway to a deeper understanding of fundamental mathematical principles and their far-reaching implications. By understanding the HCF and its related concepts, you unlock a deeper appreciation for the elegance and power of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 24 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.