Highest Common Factor Of 32 And 40
News Co
Apr 07, 2025 · 5 min read
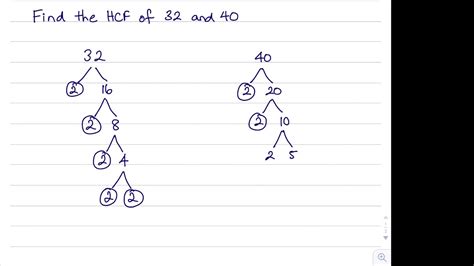
Table of Contents
Finding the Highest Common Factor (HCF) of 32 and 40: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in number theory with applications across various fields, from cryptography to computer science. This article delves deep into the process of determining the HCF of 32 and 40, exploring multiple methods and highlighting the underlying mathematical principles. We'll also touch upon the broader significance of HCF and its practical uses.
Understanding Highest Common Factor (HCF)
Before we jump into calculating the HCF of 32 and 40, let's solidify our understanding of the concept. The HCF of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that is a common factor to all the given numbers.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest among these common factors is 6; therefore, the HCF of 12 and 18 is 6.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the HCF. It involves expressing each number as a product of its prime factors. Prime factors are numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's apply this method to find the HCF of 32 and 40:
1. Prime Factorization of 32:
32 can be expressed as: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
2. Prime Factorization of 40:
40 can be expressed as: 2 x 2 x 2 x 5 = 2<sup>3</sup> x 5
3. Identifying Common Factors:
Now, let's identify the common prime factors in both factorizations. Both 32 and 40 share three factors of 2 (2<sup>3</sup>).
4. Calculating the HCF:
The HCF is the product of the common prime factors raised to the lowest power. In this case, the HCF is 2<sup>3</sup> = 8.
Therefore, the highest common factor of 32 and 40 is 8.
Method 2: Listing Factors
This method is simpler for smaller numbers but can become cumbersome for larger ones. It involves listing all the factors of each number and then identifying the largest common factor.
1. Factors of 32: 1, 2, 4, 8, 16, 32
2. Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
3. Common Factors: 1, 2, 4, 8
4. Highest Common Factor: The largest common factor is 8.
Therefore, using the listing factors method, the HCF of 32 and 40 is again 8.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal. That equal number is the HCF.
Let's apply the Euclidean algorithm to 32 and 40:
-
Start with the larger number (40) and the smaller number (32): 40 and 32
-
Subtract the smaller number from the larger number: 40 - 32 = 8
-
Replace the larger number with the result (8): 8 and 32
-
Repeat the subtraction: 32 - 8 = 24
-
Replace the larger number: 8 and 24
-
Repeat: 24 - 8 = 16
-
Replace: 8 and 16
-
Repeat: 16 - 8 = 8
-
Replace: 8 and 8
The numbers are now equal, indicating that the HCF is 8.
Method 4: Using the Formula (for two numbers only)
While not as intuitive as the other methods, there's a formula you can utilize for finding the HCF of two numbers, 'a' and 'b', specifically if you know their LCM (Least Common Multiple):
HCF(a, b) = (a * b) / LCM(a, b)
First, we need to find the LCM of 32 and 40. The prime factorization method is helpful here.
Prime Factorization of 32: 2<sup>5</sup>
Prime Factorization of 40: 2<sup>3</sup> x 5
To find the LCM, we take the highest power of each prime factor present in either number: 2<sup>5</sup> x 5 = 160
Now, let's plug the values into the formula:
HCF(32, 40) = (32 * 40) / 160 = 1280 / 160 = 8
Applications of HCF
The HCF finds applications in various areas:
-
Simplifying Fractions: Finding the HCF of the numerator and denominator allows us to simplify fractions to their lowest terms. For example, 32/40 simplifies to 8/10 and further to 4/5 (using the HCF of 8).
-
Solving Word Problems: Many word problems involving division and grouping require finding the HCF to determine the largest possible size of groups or the greatest number of items that can be divided equally. Imagine distributing 32 apples and 40 oranges equally amongst baskets - the HCF (8) tells us the maximum number of baskets possible, with each containing 4 apples and 5 oranges.
-
Cryptography: Number theory and concepts like HCF are crucial in modern cryptography. Algorithms depend heavily on the properties of prime numbers and their interactions.
-
Computer Science: Algorithms in computer science use HCF and related concepts for various tasks, such as optimizing data structures and simplifying computations.
Conclusion
Finding the HCF of 32 and 40, as demonstrated through multiple methods, is more than just a mathematical exercise. It showcases fundamental principles of number theory with practical implications across different domains. Understanding these methods equips you with valuable skills applicable in problem-solving and various advanced mathematical concepts. Choosing the most efficient method often depends on the size of the numbers involved – the Euclidean algorithm stands out for its efficiency with larger numbers, while prime factorization provides a clear understanding of the underlying structure of the numbers. Regardless of the method used, the result remains consistent: the HCF of 32 and 40 is 8.
Latest Posts
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 32 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.