How Do You Convert A Fraction Into A Whole Number
News Co
Apr 05, 2025 · 5 min read
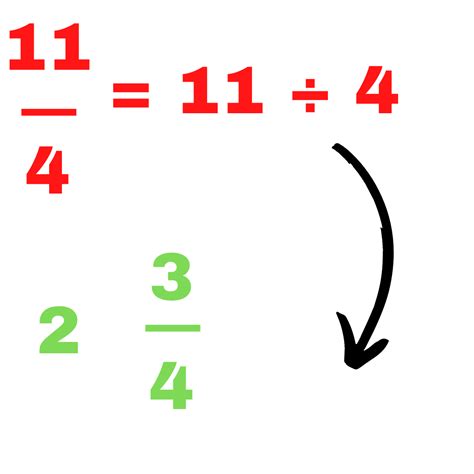
Table of Contents
How Do You Convert a Fraction into a Whole Number? A Comprehensive Guide
Converting a fraction into a whole number isn't always possible, as fractions represent parts of a whole. However, we can simplify fractions to their lowest terms, and sometimes a fraction will represent a whole number in disguise. This guide will explore the different scenarios and techniques involved in dealing with fractions and aiming for whole number representations.
Understanding Fractions
Before diving into conversions, let's solidify our understanding of fractions. A fraction is a representation of a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 3/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (3) indicates we're considering three of those parts.
When Can a Fraction Be Converted to a Whole Number?
A fraction can be converted to a whole number only when the numerator is a multiple of the denominator. In other words, the numerator is divisible by the denominator without leaving a remainder. This means the fraction represents a complete whole or multiples of a whole.
Example:
- 6/3: The numerator (6) is divisible by the denominator (3) with no remainder (6 ÷ 3 = 2). This fraction represents the whole number 2.
Methods for Converting Fractions to Whole Numbers
There are several approaches to converting a fraction to a whole number (when possible):
1. Division
The most straightforward method is simple division. Divide the numerator by the denominator. If the division results in a whole number with no remainder, the fraction is equivalent to that whole number.
Example:
-
12/4: 12 ÷ 4 = 3. Therefore, 12/4 equals 3.
-
25/5: 25 ÷ 5 = 5. Therefore, 25/5 equals 5.
2. Simplification (Reduction)
Sometimes, a fraction might not appear to directly convert to a whole number, but simplification can reveal a whole number equivalent. Simplification involves finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by the GCD. This process reduces the fraction to its simplest form.
Example:
-
15/5: The GCD of 15 and 5 is 5. Dividing both numerator and denominator by 5 results in 3/1, which equals 3.
-
20/4: The GCD of 20 and 4 is 4. Dividing both by 4 simplifies the fraction to 5/1, which equals 5.
Finding the Greatest Common Divisor (GCD):
There are several ways to find the GCD:
-
Listing Factors: List all factors of both the numerator and the denominator. The largest common factor is the GCD.
-
Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
-
Euclidean Algorithm: A more efficient method for larger numbers, involving repeated division with remainders.
3. Identifying Multiples
If you recognize that the numerator is a multiple of the denominator, you can directly convert the fraction.
Example:
-
18/6: You know that 18 is a multiple of 6 (6 x 3 = 18). Therefore, 18/6 = 3.
-
35/7: Recognizing that 35 is a multiple of 7 (7 x 5 = 35), you can immediately determine that 35/7 = 5.
Dealing with Fractions That Cannot Be Converted to Whole Numbers
Not all fractions can be converted into whole numbers. If the numerator is not a multiple of the denominator, the result of the division will be a decimal or a mixed number (a whole number and a fraction).
Examples:
-
7/3: 7 ÷ 3 = 2.333... (a decimal)
-
5/2: 5 ÷ 2 = 2 1/2 (a mixed number)
Mixed Numbers and Improper Fractions
A mixed number combines a whole number and a proper fraction (numerator < denominator). An improper fraction has a numerator greater than or equal to the denominator. Improper fractions can be converted to mixed numbers, and sometimes (as shown above), mixed numbers might represent a whole number after simplification.
Converting Improper Fractions to Mixed Numbers:
- Divide the numerator by the denominator.
- The quotient (result of the division) is the whole number part of the mixed number.
- The remainder is the numerator of the fractional part of the mixed number.
- The denominator remains the same.
Example:
-
7/3: 7 ÷ 3 = 2 with a remainder of 1. Therefore, 7/3 = 2 1/3.
-
11/4: 11 ÷ 4 = 2 with a remainder of 3. Therefore, 11/4 = 2 3/4.
Converting Mixed Numbers to Improper Fractions:
- Multiply the whole number by the denominator.
- Add the result to the numerator.
- Keep the same denominator.
Example:
-
2 1/3: (2 x 3) + 1 = 7. Therefore, 2 1/3 = 7/3.
-
3 2/5: (3 x 5) + 2 = 17. Therefore, 3 2/5 = 17/5.
Practical Applications
Understanding fraction-to-whole-number conversions is crucial in various real-world scenarios:
-
Cooking: Following recipes often requires understanding fractional measurements and converting them to whole numbers or simpler fractions for easier measurement.
-
Construction: Accurate measurements in construction rely heavily on understanding fractions and their relationship to whole numbers.
-
Finance: Calculating proportions, percentages, and shares in finance involves working with fractions and potentially converting them to whole numbers for easier interpretation.
-
Data Analysis: Simplifying data representations through fractions and converting to whole numbers can make data easier to interpret and visualize.
Advanced Concepts and Further Exploration
For more advanced applications, consider exploring these concepts:
-
Rational Numbers: Fractions are a subset of rational numbers. Understanding the properties of rational numbers expands the possibilities of fraction manipulation.
-
Continued Fractions: A way of representing numbers as a sum of fractions, which can be valuable in approximation and other mathematical applications.
-
Algebraic Fractions: Involving variables alongside numbers, algebraic fractions are essential in algebra and calculus.
Conclusion
Converting a fraction into a whole number is a fundamental mathematical skill. While it's not always possible, understanding when a conversion is possible and applying the appropriate methods—division, simplification, or recognizing multiples—are crucial skills for problem-solving in many areas of life. Mastering these concepts lays the foundation for more advanced mathematical pursuits. Remember to always check if the numerator is divisible by the denominator to determine if a whole number conversion is achievable. If not, embrace the decimal or mixed number representation as equally valid and often more practical for real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Convert A Fraction Into A Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.