How Do You Find Perimeter Of A Triangle
News Co
Apr 04, 2025 · 5 min read
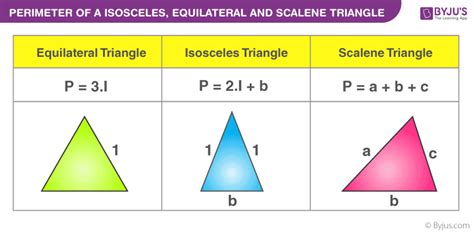
Table of Contents
How Do You Find the Perimeter of a Triangle? A Comprehensive Guide
The perimeter of any shape is simply the total distance around its exterior. For triangles, this means adding up the lengths of all three sides. While seemingly straightforward, understanding how to find the perimeter of a triangle involves various approaches and considerations, particularly when dealing with different types of triangles and limited information. This comprehensive guide will delve into the various methods, providing you with a complete understanding of how to calculate the perimeter of a triangle, regardless of the information you have available.
Understanding Triangles: Types and Properties
Before diving into the calculations, let's refresh our understanding of triangles. Triangles are classified based on their side lengths and angles:
1. Based on Side Lengths:
- Equilateral Triangle: All three sides are equal in length.
- Isosceles Triangle: Two sides are equal in length.
- Scalene Triangle: All three sides have different lengths.
2. Based on Angles:
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
Understanding these classifications helps in choosing the most appropriate method for calculating the perimeter, particularly when dealing with limited information.
Methods for Finding the Perimeter of a Triangle
The most fundamental method for finding the perimeter involves directly adding the lengths of all three sides. However, we often encounter situations where we don't have all three side lengths readily available. Let's explore various scenarios and their respective solutions:
1. Knowing All Three Side Lengths: The Direct Method
This is the simplest scenario. If you know the lengths of all three sides (let's call them a, b, and c), the perimeter (P) is calculated as:
P = a + b + c
For example, if a triangle has sides of length 5 cm, 7 cm, and 9 cm, its perimeter is:
P = 5 cm + 7 cm + 9 cm = 21 cm
2. Knowing Two Sides and the Included Angle: Using the Law of Cosines
When you know two sides and the angle between them (let's say sides a and b, and angle C), you can use the Law of Cosines to find the length of the third side (c) before calculating the perimeter. The Law of Cosines states:
c² = a² + b² - 2ab cos(C)
After calculating c, you can then use the direct method (P = a + b + c) to find the perimeter.
Example: Consider a triangle with sides a = 6 cm, b = 8 cm, and the included angle C = 60 degrees.
- Calculate c: c² = 6² + 8² - 2(6)(8)cos(60°) = 36 + 64 - 96(0.5) = 40. Therefore, c = √40 ≈ 6.32 cm.
- Calculate the perimeter: P = 6 cm + 8 cm + 6.32 cm ≈ 20.32 cm
3. Knowing Two Angles and One Side: Using the Law of Sines
If you know two angles (A and B) and the side opposite one of them (a), you can use the Law of Sines to find the other two sides. The Law of Sines states:
a/sin(A) = b/sin(B) = c/sin(C)
Since the sum of angles in a triangle is always 180 degrees, you can find the third angle (C = 180° - A - B). Then, you can use the Law of Sines to find the lengths of sides b and c, and finally, calculate the perimeter using the direct method.
Example: Suppose a triangle has angle A = 45°, angle B = 60°, and side a = 10 cm.
- Find angle C: C = 180° - 45° - 60° = 75°
- Find side b: b = a * sin(B) / sin(A) = 10 * sin(60°) / sin(45°) ≈ 12.25 cm
- Find side c: c = a * sin(C) / sin(A) = 10 * sin(75°) / sin(45°) ≈ 13.66 cm
- Calculate the perimeter: P = 10 cm + 12.25 cm + 13.66 cm ≈ 35.91 cm
4. Using Heron's Formula (When all three sides are known or calculable)
Heron's formula provides a method to calculate the area of a triangle when all three side lengths are known. While it doesn't directly give the perimeter, it's a useful tool, particularly when combined with other methods to indirectly find side lengths. Heron's formula states:
Area = √[s(s-a)(s-b)(s-c)]
where s is the semi-perimeter: s = (a + b + c) / 2
While not directly calculating the perimeter, once you have calculated the area using this formula, in conjunction with other methods, you may indirectly find the perimeter.
5. Special Triangles: Shortcuts and Simplifications
For specific types of triangles, there are shortcuts:
- Equilateral Triangle: If all sides are equal in length (a), the perimeter is simply P = 3a.
- Isosceles Triangle: If two sides are equal (a), and the third side is b, the perimeter is P = 2a + b.
Practical Applications and Real-World Examples
Understanding how to find the perimeter of a triangle is crucial in various fields:
- Construction and Engineering: Calculating the perimeter is essential in designing and building structures, laying out foundations, and estimating material requirements.
- Surveying and Land Measurement: Determining the perimeter of land plots is crucial for property boundaries and legal documentation.
- Cartography and Mapmaking: Accurate perimeter calculations are essential in representing geographical features on maps.
- Computer Graphics and Design: Perimeter calculations are used in creating geometric shapes and designs in computer-aided design (CAD) software.
Advanced Concepts and Further Exploration
For more advanced scenarios, you might encounter problems involving:
- Triangles inscribed within or circumscribed around circles: These problems often require using geometric theorems and properties of circles.
- Triangles in three-dimensional space: Finding the perimeter involves using vector calculations and spatial geometry.
- Dynamic triangles: Problems might involve triangles whose sides are changing over time, requiring calculus to analyze the rate of change of the perimeter.
Conclusion
Finding the perimeter of a triangle, while seemingly basic, encompasses various methods and considerations depending on the information provided. Whether you use the direct method, the Law of Cosines, the Law of Sines, Heron's formula, or shortcuts for special triangles, understanding these approaches empowers you to solve a wide range of problems across numerous disciplines. Remember to carefully analyze the given information and choose the most efficient and accurate method to calculate the perimeter, ensuring that your calculations are precise and relevant to the specific context. This guide serves as a solid foundation for tackling triangle perimeter calculations and opens doors to exploring more advanced geometric concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Find Perimeter Of A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.