How Do You Find The Diagonal Of A Parallelogram
News Co
Apr 06, 2025 · 6 min read
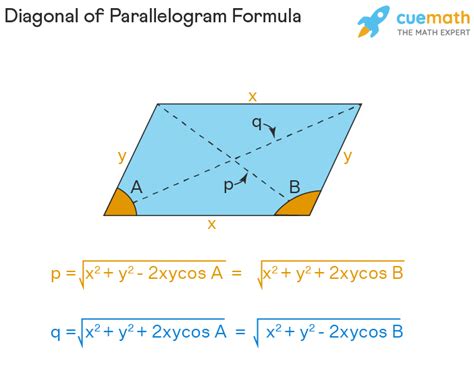
Table of Contents
How to Find the Diagonal of a Parallelogram: A Comprehensive Guide
Finding the diagonal of a parallelogram might seem like a simple geometry problem, but understanding the various methods and their applications is crucial for a solid grasp of geometry and its practical uses. This comprehensive guide will walk you through different approaches, from basic trigonometry to more advanced vector methods, ensuring you have a complete understanding of this fundamental concept. We'll cover various scenarios, including knowing different parameters of the parallelogram like side lengths, angles, and area.
Understanding Parallelograms and Their Diagonals
Before diving into the methods, let's establish a firm foundation. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. This inherent property leads to several important characteristics, including:
- Opposite angles are equal: Angles A and C are equal, as are angles B and D.
- Adjacent angles are supplementary: Angles A and B add up to 180 degrees, as do angles B and C, C and D, and D and A.
- Diagonals bisect each other: The diagonals intersect at a point that divides each diagonal into two equal segments.
A parallelogram has two diagonals, each connecting opposite vertices. These diagonals play a crucial role in various geometrical calculations, and understanding their properties is essential for solving various problems.
Method 1: Using the Law of Cosines
The Law of Cosines is a powerful tool for finding the length of a side of a triangle when you know the lengths of the other two sides and the angle between them. Since a parallelogram can be divided into two congruent triangles by drawing a diagonal, we can use the Law of Cosines to find the length of the diagonal.
The Law of Cosines states: c² = a² + b² - 2ab * cos(C)
Where:
- 'c' is the length of the side opposite angle C
- 'a' and 'b' are the lengths of the other two sides
- 'C' is the angle between sides 'a' and 'b'
Applying it to a Parallelogram:
Let's say we have a parallelogram with sides 'a' and 'b', and the angle between them is 'θ'. To find the diagonal 'd', we can consider one of the triangles formed by the diagonal:
- 'a' and 'b' are the sides of the triangle.
- 'θ' is the angle between 'a' and 'b'.
- 'd' is the diagonal (the side opposite θ).
Therefore, using the Law of Cosines:
d² = a² + b² - 2ab * cos(θ)
d = √(a² + b² - 2ab * cos(θ))
Example:
A parallelogram has sides of length 5 cm and 8 cm, and the angle between them is 60 degrees. Let's find the length of the diagonal:
d = √(5² + 8² - 2 * 5 * 8 * cos(60°))
d = √(25 + 64 - 80 * 0.5)
d = √(89 - 40)
d = √49
d = 7 cm
This method is particularly useful when you know the lengths of two adjacent sides and the angle between them.
Method 2: Using the Pythagorean Theorem (for Rectangles and Rhombuses)
The Pythagorean Theorem is a special case of the Law of Cosines, applicable when the angle between the sides is 90 degrees (a right angle). This means it's directly usable for finding the diagonal of a rectangle or a rhombus (a parallelogram with equal sides).
The Pythagorean Theorem states: c² = a² + b²
Where:
- 'a' and 'b' are the lengths of the two shorter sides (legs) of a right-angled triangle.
- 'c' is the length of the longest side (hypotenuse).
Applying it to Rectangles and Rhombuses:
In a rectangle, the two sides forming a right angle are adjacent sides. Thus, the diagonal acts as the hypotenuse. Similarly, in a rhombus, we can create a right-angled triangle using the half-diagonals.
Example (Rectangle):
A rectangle has sides of length 6 cm and 8 cm. The diagonal 'd' can be found as follows:
d² = 6² + 8²
d² = 36 + 64
d² = 100
d = 10 cm
Example (Rhombus): If the side length of the rhombus is 'a' and one of the diagonals is 'd1', then half the diagonal forms a right-angled triangle with the side and the other half-diagonal. With the other diagonal being 'd2':
a² = (d1/2)² + (d2/2)²
This equation allows calculating one diagonal if the side and the other diagonal are known.
Method 3: Using Vectors
Vector methods provide a more sophisticated approach, particularly useful when dealing with more complex geometric problems in higher dimensions. This method utilizes the properties of vectors to determine the diagonal's length and direction.
The Vector Approach:
Let's represent the sides of the parallelogram as vectors a and b. The diagonal connecting the endpoints of these vectors is given by the vector sum a + b. The magnitude of this resultant vector represents the length of the diagonal.
The magnitude of a vector v = (x, y) is given by ||v|| = √(x² + y²)
Therefore, the length of the diagonal 'd' is given by:
d = ||a + b|| = √((a_x + b_x)² + (a_y + b_y)²)
Where a_x and a_y are the x and y components of vector a, and b_x and b_y are the x and y components of vector b.
This method becomes particularly valuable when working in three-dimensional space or when dealing with parallelograms defined by their vertices' coordinates.
Method 4: Using the Area and the Sine Rule
If the area of the parallelogram and the lengths of its adjacent sides are known, the sine rule can be used to determine the angle between the sides. Once the angle is known, the Law of Cosines (Method 1) can then be applied to find the diagonal.
The area (A) of a parallelogram is given by:
A = ab * sin(θ)
where:
- 'a' and 'b' are the lengths of adjacent sides.
- 'θ' is the angle between the adjacent sides.
From this equation, you can find the angle:
θ = arcsin(A / (ab))
Once 'θ' is known, substitute it into the Law of Cosines to calculate the diagonal length.
Finding the Other Diagonal
Parallelograms have two diagonals. Once you've found one using the methods above, finding the second diagonal might involve similar calculations, often involving the properties of bisecting diagonals. The approach depends on the known parameters. For example:
- If the parallelogram is a rectangle: Both diagonals are equal in length.
- If the parallelogram is a rhombus: The diagonals are perpendicular bisectors of each other.
- General Parallelogram: If you know the lengths of the sides and one diagonal, you can use the properties of triangles formed by the diagonals to find the length of the second diagonal. This might involve applying the Law of Cosines to a different triangle within the parallelogram.
Practical Applications
Understanding how to find the diagonals of a parallelogram has various practical applications across multiple fields:
- Engineering: Calculating forces and stresses in structures.
- Physics: Determining vector components and resolving forces.
- Computer Graphics: Representing and manipulating 2D and 3D shapes.
- Cartography: Calculating distances and areas on maps.
- Construction: Measuring and planning building layouts.
Conclusion
Finding the diagonal of a parallelogram involves a multifaceted approach, dependent on the given parameters. From the straightforward Pythagorean theorem for rectangles and rhombuses, to the more versatile Law of Cosines and sophisticated vector methods, the choice of method depends on the information available. Mastering these methods provides a strong foundation for tackling more complex geometrical problems and understanding the practical applications of geometric principles in diverse fields. Remember to always carefully consider the given information and choose the most efficient method to solve the problem. Practice with different examples to solidify your understanding and gain confidence in applying these valuable techniques.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Find The Diagonal Of A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.