How Do You Find The Height Of A Parallelogram
News Co
Apr 06, 2025 · 5 min read
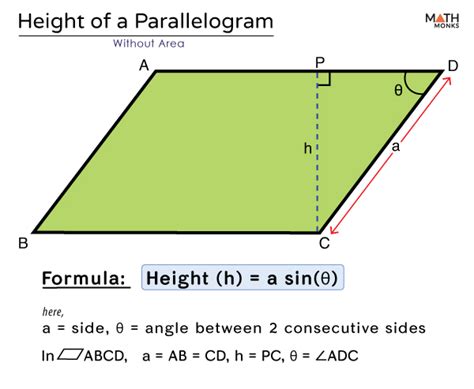
Table of Contents
How Do You Find the Height of a Parallelogram? A Comprehensive Guide
Finding the height of a parallelogram might seem straightforward, but understanding the nuances and various approaches is crucial for accurate calculations and a deeper grasp of geometric principles. This comprehensive guide explores different methods to determine the height, catering to various levels of mathematical understanding. We'll cover scenarios with known areas, base lengths, and even using trigonometry for more complex situations. Let's delve into the fascinating world of parallelograms and their heights!
Understanding the Parallelogram and its Height
A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. This seemingly simple definition opens the door to several ways we can determine its height. Unlike a rectangle where the height is simply one of the sides, the height of a parallelogram is the perpendicular distance between two parallel sides. This perpendicular distance is crucial because it's directly related to the parallelogram's area.
Key Terms:
- Base (b): Any one of the parallelogram's sides. You can choose any side as the base, but once chosen, the height must be measured perpendicular to that base.
- Height (h): The perpendicular distance between the chosen base and the opposite parallel side. It's always measured at a right angle (90 degrees) to the base.
- Area (A): The amount of space enclosed within the parallelogram. The formula for the area of a parallelogram is A = b * h.
Methods for Finding the Height of a Parallelogram
Several methods exist to determine the height of a parallelogram, depending on the information provided. Let's examine the most common approaches:
1. Using the Area and Base Length
This is the most straightforward method. If you know the area (A) and the length of the base (b), you can easily calculate the height (h) using the area formula:
A = b * h
To find the height, simply rearrange the formula:
h = A / b
Example: A parallelogram has an area of 30 square centimeters and a base of 5 centimeters. What is its height?
h = 30 cm² / 5 cm = 6 cm
The height of the parallelogram is 6 centimeters.
2. Using Trigonometry (When Angles are Known)
When the area isn't provided but you know the length of one side and an angle, trigonometry provides a powerful tool. Let's consider a parallelogram where you know the length of one side (let's call it 'a') and the angle between that side and the height (let's call this angle θ). The height (h) can be calculated using the sine function:
h = a * sin(θ)
Important Note: θ is the angle between the side 'a' and the base (not the angle between the two sides). Ensure you're using the correct angle.
Example: Imagine a parallelogram with a side length (a) of 8 cm and an angle (θ) of 30 degrees between that side and the base. What is the height?
h = 8 cm * sin(30°) = 8 cm * 0.5 = 4 cm
Therefore, the height of the parallelogram is 4 centimeters.
3. Using Coordinate Geometry
If the vertices of the parallelogram are defined by their coordinates in a Cartesian plane, you can utilize coordinate geometry to find the height.
Steps:
- Choose a base: Select any side of the parallelogram as your base.
- Find the equation of the line containing the base: Use the two points defining the chosen base to calculate the slope (m) and the y-intercept (c) of the line using the equation y = mx + c.
- Find the equation of the line perpendicular to the base: The slope of the perpendicular line (m⊥) is the negative reciprocal of the base line's slope (m⊥ = -1/m). This perpendicular line will pass through the opposite vertex of the parallelogram that is not on the chosen base.
- Find the point of intersection: Solve the simultaneous equations of the base line and the perpendicular line to find their point of intersection.
- Calculate the distance: The height is the distance between the point of intersection and the vertex of the base that is not part of the initial two points used to find the line of the base. Use the distance formula to calculate this distance: √[(x₂ - x₁)² + (y₂ - y₁)²]
This method involves more complex calculations but is invaluable when dealing with parallelograms defined by their coordinates.
4. Constructing a Right-Angled Triangle
Sometimes, the height of a parallelogram isn’t directly given. However, if you have a diagram showing the parallelogram and can draw a perpendicular line from one vertex to the opposite side, you create a right-angled triangle. This allows the application of Pythagorean theorem or trigonometric ratios to find the height.
Advanced Scenarios and Considerations
While the methods above cover common scenarios, more complex situations may arise.
- Irregular Parallelograms: The same principles apply to irregular parallelograms (those without right angles). The key is always to identify the base and measure the perpendicular height.
- Three-Dimensional Parallelograms (Parallelepipeds): In three dimensions, the concept of height becomes more nuanced. You might need to consider the height relative to different faces or axes.
- Using Vectors: Vector mathematics provides a more elegant approach to calculating heights, especially in three-dimensional space or for parallelograms defined by vector coordinates.
Practical Applications of Finding Parallelogram Heights
The ability to calculate the height of a parallelogram isn't just a theoretical exercise. It has numerous practical applications:
- Engineering: Calculating areas of parallelogram-shaped structures like roof trusses or support beams.
- Architecture: Designing buildings and spaces with parallelogram-shaped elements.
- Physics: Analyzing forces and movements in parallelogram-shaped mechanisms.
- Computer Graphics: Creating and manipulating parallelogram-shaped objects in digital environments.
- Land Surveying: Calculating land areas with parallelogram-shaped boundaries.
Conclusion: Mastering Parallelogram Height Calculations
Understanding how to find the height of a parallelogram is a fundamental skill in geometry. Whether you're using simple formulas, trigonometry, coordinate geometry, or even constructing right-angled triangles, the core principle remains consistent: the height is the perpendicular distance between parallel sides. Mastering these techniques opens up a world of opportunities to solve more complex geometrical problems and apply your knowledge to various real-world scenarios. Remember to always clearly define your base and ensure the height is perpendicular to that base for accurate calculations. By consistently applying these principles, you will confidently tackle any parallelogram height challenge that comes your way.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Find The Height Of A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.