How Do You Find The Lateral Area Of A Cone
News Co
Apr 05, 2025 · 5 min read
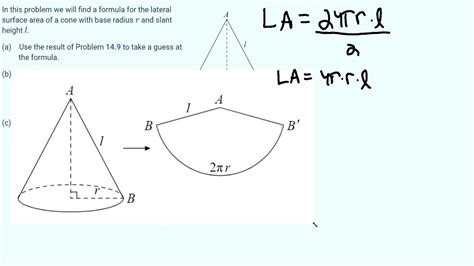
Table of Contents
How to Find the Lateral Surface Area of a Cone: A Comprehensive Guide
Understanding how to calculate the lateral surface area of a cone is crucial in various fields, from engineering and architecture to mathematics and computer graphics. This comprehensive guide will walk you through the process, explaining the underlying principles, providing step-by-step instructions, and offering practical examples. We'll also explore variations and related concepts to give you a complete understanding of this geometric calculation.
Understanding the Cone and its Components
Before diving into the calculations, let's define the key components of a cone:
- Radius (r): The distance from the center of the circular base to any point on the circumference.
- Height (h): The perpendicular distance from the apex (the top point) of the cone to the center of its base.
- Slant Height (l): The distance from the apex of the cone to any point on the circumference of its base. This is not the same as the height. The slant height, height, and radius form a right-angled triangle.
The lateral surface area (LSA) refers to the curved surface area of the cone, excluding the area of the base. The total surface area includes both the lateral surface area and the area of the circular base.
The Formula for Lateral Surface Area
The formula for the lateral surface area of a cone is:
LSA = πrl
Where:
- π (pi): Approximately 3.14159
- r: Radius of the base
- l: Slant height
This formula is derived from the concept of unfolding a cone into a sector of a circle. The arc length of this sector is the circumference of the cone's base (2πr), and the radius of the sector is the slant height (l). The area of this sector is then (1/2) * arc length * radius = (1/2) * 2πr * l = πrl.
Calculating the Slant Height
Often, you won't be given the slant height directly. Instead, you'll have the radius and height. In this case, you need to use the Pythagorean theorem to calculate the slant height. Because the radius, height, and slant height form a right-angled triangle, the theorem applies:
l² = r² + h²
Therefore, the slant height can be calculated as:
l = √(r² + h²)
This step is crucial before you can apply the main LSA formula.
Step-by-Step Calculation of Lateral Surface Area
Let's break down the calculation process with a detailed example:
Problem: Find the lateral surface area of a cone with a radius of 5 cm and a height of 12 cm.
Step 1: Calculate the slant height (l)
Using the Pythagorean theorem:
l = √(r² + h²) = √(5² + 12²) = √(25 + 144) = √169 = 13 cm
Step 2: Apply the LSA formula
LSA = πrl = π * 5 cm * 13 cm = 65π cm²
Step 3: Approximate the result
Using π ≈ 3.14159:
LSA ≈ 65 * 3.14159 cm² ≈ 204.203 cm²
Therefore, the lateral surface area of the cone is approximately 204.20 square centimeters.
Practical Applications and Examples
Understanding the lateral surface area of a cone has numerous applications:
- Packaging Design: Determining the amount of material needed to create conical containers or packaging. This is crucial for minimizing waste and optimizing production costs.
- Civil Engineering: Calculating the surface area of conical structures like silos or funnels for material handling. This helps in material estimation and structural design.
- Architectural Design: Designing conical roofs or other architectural elements. Accurate LSA calculation ensures proper material estimation and structural integrity.
- Manufacturing: Calculating the surface area of conical parts for machining, coating, or other manufacturing processes. This allows for precise material usage and efficient production.
- Computer Graphics: Creating realistic 3D models of conical objects requires accurate LSA calculation for accurate rendering and texturing.
Example 2: A Real-World Scenario
Imagine you're designing a paper party hat. You want the hat to have a radius of 7cm and a height of 10cm. To determine the amount of paper needed, you calculate the lateral surface area:
Step 1: Calculate the slant height:
l = √(7² + 10²) = √(49 + 100) = √149 ≈ 12.21 cm
Step 2: Calculate the LSA:
LSA = πrl = π * 7cm * 12.21cm ≈ 268.5 cm²
You would need approximately 268.5 square centimeters of paper to make the party hat.
Variations and Extensions
The basic cone formula can be extended to more complex shapes:
- Frustum of a cone: A frustum is the portion of a cone remaining after its top is cut off by a plane parallel to the base. The LSA calculation for a frustum involves the radii of both the top and bottom bases and the slant height of the frustum. The formula becomes more complex but follows similar geometric principles.
- Conical sections: Understanding the LSA of a cone is foundational to understanding the properties of conic sections such as ellipses, parabolas, and hyperbolas.
Troubleshooting and Common Mistakes
- Confusing height and slant height: Remember that the height and slant height are different. Always use the slant height in the LSA formula.
- Incorrect use of the Pythagorean theorem: Double-check your calculations when applying the Pythagorean theorem to find the slant height.
- Unit consistency: Ensure all measurements (radius, height, slant height) are in the same units before applying the formula to avoid errors.
Conclusion: Mastering Cone Lateral Surface Area
Calculating the lateral surface area of a cone is a fundamental skill with wide-ranging applications. By understanding the formula, applying the Pythagorean theorem correctly, and practicing with different examples, you can confidently tackle this geometric calculation. Remember to always double-check your units and calculations to ensure accuracy. This comprehensive guide provides you with the knowledge and tools to master this important concept in geometry. From designing party hats to constructing complex engineering projects, a solid grasp of cone lateral surface area is invaluable. With practice and careful attention to detail, you can become proficient in these calculations and apply them effectively in various contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Find The Lateral Area Of A Cone . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.