How Do You Find The Perimeter Of A Hexagon
News Co
Apr 08, 2025 · 5 min read
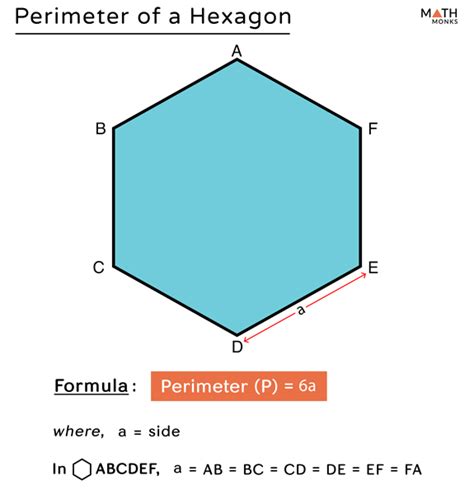
Table of Contents
How Do You Find the Perimeter of a Hexagon? A Comprehensive Guide
Finding the perimeter of a hexagon might seem daunting at first, but with a clear understanding of its properties and the right formulas, it becomes a straightforward task. This comprehensive guide will explore various methods to calculate the perimeter of a hexagon, catering to different levels of mathematical understanding. We'll delve into regular hexagons, irregular hexagons, and even explore real-world applications where calculating a hexagon's perimeter is crucial.
Understanding Hexagons: The Basics
Before we jump into calculations, let's refresh our understanding of hexagons. A hexagon is a polygon with six sides. The perimeter of any polygon is simply the sum of the lengths of all its sides. However, calculating the perimeter becomes easier if we know the type of hexagon we're dealing with.
Regular Hexagons: The Simple Case
A regular hexagon is a special type of hexagon where all six sides are equal in length, and all six interior angles are equal (each measuring 120 degrees). This symmetry makes calculating the perimeter significantly simpler.
Formula for a Regular Hexagon:
The perimeter (P) of a regular hexagon is given by the formula:
P = 6 * s
where 's' represents the length of one side.
Example:
If a regular hexagon has a side length of 5 cm, its perimeter is:
P = 6 * 5 cm = 30 cm
Irregular Hexagons: A More Complex Approach
An irregular hexagon has sides of varying lengths. There's no single, neat formula like the one for regular hexagons. To find the perimeter of an irregular hexagon, you must measure or be given the length of each of its six sides.
Calculating the Perimeter of an Irregular Hexagon:
The perimeter (P) of an irregular hexagon is found by adding the lengths of all six sides:
P = a + b + c + d + e + f
where a, b, c, d, e, and f represent the lengths of the six sides.
Example:
If an irregular hexagon has sides with lengths 2 cm, 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm, its perimeter is:
P = 2 cm + 3 cm + 4 cm + 5 cm + 6 cm + 7 cm = 27 cm
Advanced Techniques and Considerations
While the above methods are sufficient for many scenarios, let's explore some more advanced techniques and scenarios that require a deeper understanding of geometry.
Using Trigonometry for Irregular Hexagons
For complex irregular hexagons where side lengths aren't directly given, trigonometry can be a powerful tool. If you know some angles and side lengths, you can use trigonometric functions (sine, cosine, tangent) and the laws of sines and cosines to calculate the missing side lengths and ultimately determine the perimeter.
This approach often involves breaking the hexagon down into smaller triangles and applying trigonometric principles to each triangle to find unknown sides. This is a more advanced technique requiring a strong foundation in trigonometry.
Hexagons Inscribed in Circles: A Geometric Approach
A hexagon inscribed in a circle is a hexagon whose vertices all lie on the circumference of a circle. In the specific case of a regular hexagon inscribed in a circle, the relationship between the side length ('s') and the radius ('r') of the circle is very simple:
s = r
Therefore, the perimeter of a regular hexagon inscribed in a circle is:
P = 6r
This relationship is a direct consequence of the fact that a regular hexagon can be divided into six equilateral triangles.
Real-World Applications: Where Hexagons Matter
Hexagons appear frequently in various real-world applications, and understanding how to calculate their perimeter is crucial in many fields:
-
Engineering: In structural engineering, hexagons are sometimes used in designs due to their strength and stability. Calculating the perimeter is essential for material estimations and structural analysis. Think of hexagonal nuts and bolts, or even honeycomb structures used in aerospace engineering.
-
Architecture: Hexagonal designs are incorporated in building structures, window designs, and floor tiling patterns. Knowing the perimeter is essential for accurate measurements during construction and material purchasing.
-
Nature: Honeycomb structures, created by bees, are composed of perfectly regular hexagonal cells. Understanding the perimeter of these cells is relevant to biological studies.
-
Game Design: In various games (like board games or video games), hexagons are used for map grids or game tiles. Calculating perimeters might be needed for pathfinding algorithms or resource management within the game.
-
Graphic Design & Art: Artists and designers frequently use hexagonal shapes in their creations. Precise calculations of perimeter are important for accurate scaling and proportions.
Troubleshooting and Common Mistakes
While calculating the perimeter of a hexagon is relatively straightforward, certain common mistakes can lead to inaccurate results:
-
Confusing regular and irregular hexagons: Remember to use the appropriate formula based on whether the hexagon is regular or irregular.
-
Incorrect measurement of sides: Always ensure accurate measurements, especially when dealing with irregular hexagons. A small error in measuring one side can significantly impact the final perimeter calculation.
-
Forgetting to add all sides (irregular hexagons): When working with irregular hexagons, make sure to account for all six sides in the summation. It's easy to miss a side, leading to an incorrect perimeter.
-
Misapplication of trigonometry: When using trigonometry, ensure you're using the correct trigonometric functions and formulas for the specific problem. A misunderstanding of trigonometric principles can lead to significant errors.
Conclusion: Mastering Hexagon Perimeters
Calculating the perimeter of a hexagon is a fundamental concept in geometry with applications across various disciplines. While regular hexagons offer a simple formula, irregular hexagons require a more comprehensive approach, possibly incorporating trigonometry. By understanding the properties of hexagons and mastering the appropriate calculation methods, you equip yourself with a valuable skill for tackling geometric problems and real-world challenges involving these fascinating six-sided shapes. Remember to always double-check your measurements and calculations to ensure accuracy. With practice and attention to detail, you'll master the art of finding hexagon perimeters with confidence.
Latest Posts
Latest Posts
-
What Is 25 Off Of 50
Apr 08, 2025
-
All Local Maximum Values Of F
Apr 08, 2025
-
Examples Of Polynomials And Non Polynomials
Apr 08, 2025
-
How Many Water Bottles Equal A Gallon Of Water
Apr 08, 2025
-
Is 101 A Prime Or Composite Number
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Perimeter Of A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.