How Do You Multiply Mixed Numbers By Whole Numbers
News Co
Apr 07, 2025 · 6 min read
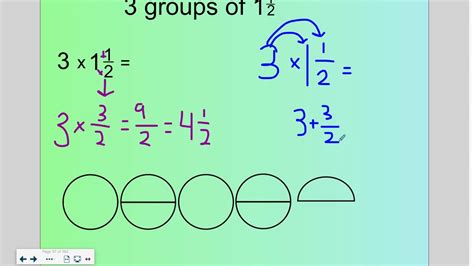
Table of Contents
How to Multiply Mixed Numbers by Whole Numbers: A Comprehensive Guide
Multiplying mixed numbers by whole numbers might seem daunting at first, but with a structured approach and a solid understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through various methods, offering clear explanations and practical examples to solidify your understanding. We'll explore different techniques, catering to various learning styles, ensuring you master this essential arithmetic skill.
Understanding Mixed Numbers and Whole Numbers
Before diving into the multiplication process, let's refresh our understanding of the key components: mixed numbers and whole numbers.
Whole Numbers: These are the numbers we use for counting, starting from zero and extending infinitely (0, 1, 2, 3...). They don't contain fractions or decimals.
Mixed Numbers: These numbers combine a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit.
Understanding the composition of mixed numbers is crucial for effective multiplication. We'll explore how to leverage this structure to simplify calculations.
Method 1: Converting to Improper Fractions
This is arguably the most common and efficient method for multiplying mixed numbers by whole numbers. It involves transforming the mixed number into an improper fraction (where the numerator is larger than or equal to the denominator) before performing the multiplication.
Steps:
-
Convert the mixed number to an improper fraction: To do this, multiply the whole number by the denominator of the fraction, add the numerator, and keep the same denominator.
Example: Let's convert 2 ¾ to an improper fraction:
(2 x 4) + 3 = 11. The improper fraction is 11/4.
-
Multiply the improper fraction by the whole number: Multiply the numerators together and then the denominators.
Example: If we want to calculate 2 ¾ x 5, we would multiply 11/4 x 5/1:
(11 x 5) / (4 x 1) = 55/4
-
Convert the result back to a mixed number (if needed): To express the answer as a mixed number, divide the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction, keeping the same denominator.
Example: Converting 55/4 back to a mixed number:
55 ÷ 4 = 13 with a remainder of 3. Therefore, 55/4 = 13 ¾
Example Problem: Calculate 3 2/5 x 6
-
Convert 3 2/5 to an improper fraction: (3 x 5) + 2 = 17. The improper fraction is 17/5.
-
Multiply: 17/5 x 6/1 = 102/5
-
Convert back to a mixed number: 102 ÷ 5 = 20 with a remainder of 2. Therefore, 102/5 = 20 2/5
Therefore, 3 2/5 x 6 = 20 2/5
Method 2: Distributive Property
The distributive property of multiplication allows us to break down the problem into smaller, more manageable parts. This method is particularly helpful for those who prefer working with whole numbers and fractions separately.
Steps:
-
Distribute the whole number to both parts of the mixed number: Multiply the whole number by the whole number part of the mixed number, then multiply the whole number by the fractional part.
Example: For 2 ¾ x 5, we would calculate:
(2 x 5) + (¾ x 5)
-
Simplify and combine: Calculate each multiplication individually, then add the results together.
Example: Continuing with our example:
(2 x 5) + (¾ x 5) = 10 + 15/4
-
Convert to a mixed number (if necessary): Convert the improper fraction to a mixed number and combine with the whole number.
Example: Converting 15/4 to a mixed number gives 3 ¾. Therefore, 10 + 3 ¾ = 13 ¾
Example Problem: Calculate 4 1/3 x 7
-
Distribute: (4 x 7) + (1/3 x 7)
-
Simplify: 28 + 7/3
-
Convert and combine: 7/3 = 2 1/3. Therefore, 28 + 2 1/3 = 30 1/3
Therefore, 4 1/3 x 7 = 30 1/3
Method 3: Using Decimal Representation
This method involves converting the mixed number into a decimal and then performing the multiplication. This approach is suitable when dealing with fractions that have denominators that are easily converted to decimals (e.g., 10, 100, 1000). However, it might introduce rounding errors with fractions that result in non-terminating decimals.
Steps:
-
Convert the mixed number to a decimal: Divide the numerator of the fraction by the denominator and add the result to the whole number.
Example: Converting 2 ¾ to a decimal: ¾ = 0.75, so 2 ¾ = 2.75
-
Multiply the decimal by the whole number: Perform standard decimal multiplication.
Example: 2.75 x 5 = 13.75
Example Problem: Calculate 1 1/2 x 4
-
Convert 1 1/2 to a decimal: 1/2 = 0.5, so 1 1/2 = 1.5
-
Multiply: 1.5 x 4 = 6
Therefore, 1 1/2 x 4 = 6
Choosing the Right Method
The best method depends on your personal preference and the specific problem. The improper fraction method is generally efficient and avoids potential rounding errors, making it a good all-around choice. The distributive property is useful for visualizing the multiplication process, while the decimal method is suitable when dealing with fractions easily converted to decimals.
Practicing and Troubleshooting
Consistent practice is key to mastering this skill. Start with simple problems and gradually increase the complexity. Here are some tips for troubleshooting:
- Double-check your conversions: Ensure you've accurately converted mixed numbers to improper fractions or decimals. A small error in this step can significantly affect the final answer.
- Simplify fractions: Whenever possible, simplify fractions before and after multiplication to reduce the size of the numbers you're working with and make calculations easier.
- Use estimation: Before starting the calculation, estimate the answer to check if your final result is reasonable. This can help identify potential errors.
- Break down complex problems: If you're struggling with a particularly challenging problem, break it down into smaller, more manageable steps.
Real-World Applications
Multiplying mixed numbers by whole numbers is a fundamental skill with broad applications in various real-world scenarios. Here are a few examples:
- Cooking and Baking: Scaling up recipes often involves multiplying mixed number measurements (e.g., doubling a recipe that calls for 2 ½ cups of flour).
- Construction and Engineering: Calculating material quantities, such as the amount of lumber needed for a project, frequently involves multiplying mixed numbers.
- Sewing and Quilting: Determining fabric requirements for sewing projects often involves working with mixed number measurements.
- Finance and Budgeting: Calculating expenses or income based on fractional amounts requires the ability to multiply mixed numbers.
Conclusion
Mastering the multiplication of mixed numbers by whole numbers is a vital skill for everyday life and academic success. By understanding the underlying principles and practicing the different methods outlined in this guide, you'll build confidence and proficiency in tackling these calculations effectively. Remember to choose the method that best suits your learning style and the specific problem at hand. With consistent practice and a strategic approach, you'll become adept at this essential arithmetic skill. Remember to always check your work and use estimation to verify your results. Good luck!
Latest Posts
Related Post
Thank you for visiting our website which covers about How Do You Multiply Mixed Numbers By Whole Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.