How Many 1/3 Are In 6
News Co
Apr 23, 2025 · 5 min read
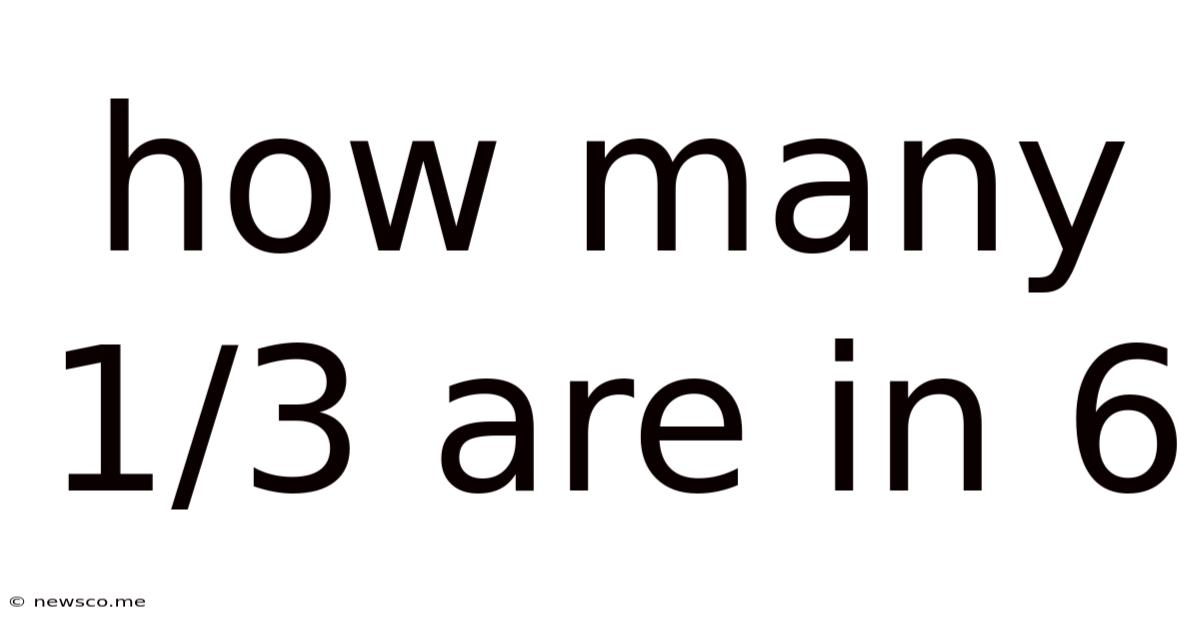
Table of Contents
How Many 1/3s Are in 6? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 1/3s are in 6?", opens the door to a fascinating exploration of fractions, division, and the underlying mathematical concepts that govern them. While the answer might seem immediately obvious to some, a thorough understanding requires delving into the mechanics of fraction manipulation and their real-world applications. This article will not only provide the solution but also illuminate the process, equipping you with the tools to tackle similar problems with confidence.
Understanding the Problem: Fractions and Division
The question, "How many 1/3s are in 6?", is essentially asking us to perform a division problem. We're dividing the whole number 6 by the fraction 1/3. This can be expressed mathematically as:
6 ÷ (1/3)
This representation might seem intimidating at first, but let's break it down. The core concept revolves around understanding what a fraction represents. 1/3 signifies one part out of three equal parts of a whole. The question, therefore, asks how many times this one-third portion fits into the whole number 6.
Method 1: Reciprocals and Multiplication
The most efficient way to divide by a fraction is to multiply by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of 1/3 is 3/1, or simply 3. Therefore, our problem transforms into:
6 x (3/1) = 6 x 3 = 18
Therefore, there are 18 one-thirds in 6.
This method elegantly bypasses the complexities of direct division with fractions, streamlining the calculation and offering a clear, concise solution. Understanding reciprocals is a cornerstone of working with fractions, and this method highlights its practical application.
Method 2: Visual Representation
For a more intuitive understanding, let's visualize the problem. Imagine a rectangular bar representing the whole number 6. Now, divide this bar into thirds. Each third represents 1/3.
[Insert Image Here: A rectangular bar divided into 18 equal sections, with each section labeled as 1/3. The first three sections are grouped together, then the next three, and so on, until all 18 sections are visually grouped into six sets of three.]
You'll quickly see that you can fit three one-thirds into each unit of 1. Since there are six units (representing the whole number 6), you can fit three one-thirds into each of those six units, leading to a total of 18 one-thirds.
This visual approach provides a concrete representation of the abstract mathematical concept, making it easier to grasp for those who benefit from visual aids. It solidifies the understanding that the answer of 18 isn't just a numerical result, but a tangible representation of how many times 1/3 fits into 6.
Method 3: Converting to Improper Fractions
Another approach involves converting the whole number 6 into an improper fraction with a denominator of 3. This allows us to perform division directly using the fractions.
To convert 6 into a fraction with a denominator of 3, we multiply 6 by 3/3 (which equals 1, so it doesn't change the value):
6 x (3/3) = 18/3
Now, our division problem becomes:
(18/3) ÷ (1/3)
When dividing fractions, we multiply by the reciprocal of the second fraction:
(18/3) x (3/1) = 54/3 = 18
This method, while slightly more complex than using reciprocals directly, reinforces the concept of fraction equivalence and manipulation, further strengthening your understanding of fraction arithmetic.
Real-World Applications: Where Do We Use This?
The seemingly simple concept of dividing a whole number by a fraction has far-reaching applications in various real-world scenarios:
-
Baking and Cooking: Recipes often require fractional measurements. If a recipe calls for 1/3 cup of sugar per serving and you want to make 6 servings, this calculation will tell you how much total sugar you need.
-
Construction and Measurement: In construction projects, precise measurements are critical. If a project requires pieces of wood that are 1/3 of a meter long and you need six such pieces, this calculation helps determine the total length of wood required.
-
Resource Allocation: Dividing resources among several groups often involves fractions. Imagine distributing 6 liters of water equally among three groups. Each group would receive 2 liters, which is equivalent to 6 ÷ (1/3) = 18 (thirds of a liter) and each group gets 6 thirds.
-
Data Analysis and Statistics: Many statistical calculations involve working with fractions and percentages. Understanding how fractions work is fundamental to interpreting and analyzing data effectively.
-
Finance and Investments: Calculations involving shares, interest rates, and investment returns frequently involve fractions. Determining the number of shares required, based on fractional ownership, relies heavily on such calculations.
These examples showcase how fundamental an understanding of fraction division is in various fields. It transcends the realm of abstract mathematics and becomes a practical tool for solving real-world problems.
Extending the Concept: More Complex Problems
The principles discussed here can be extended to solve more complex problems involving fractions and division. Consider the following:
-
How many 2/3s are in 6? The approach remains the same. You would divide 6 by 2/3, which is equivalent to multiplying 6 by 3/2: 6 x (3/2) = 9.
-
How many 1/4s are in 6? Divide 6 by 1/4, which is the same as multiplying 6 by 4: 6 x 4 = 24.
-
How many 5/8 are in 2? Divide 2 by 5/8, which is the same as multiplying 2 by 8/5: 2 x (8/5) = 16/5 = 3.2
By mastering the core principles of reciprocal multiplication and fraction manipulation, you can confidently tackle a wide range of similar problems involving fractions and division.
Conclusion: Mastering Fractions for Real-World Success
The seemingly simple question of "How many 1/3s are in 6?" provides a springboard for a deeper understanding of fractions and their applications in various aspects of life. From baking to construction to finance, the ability to confidently manipulate and divide fractions is an invaluable skill. By understanding the methods of reciprocal multiplication and visual representation, you can not only solve this specific problem but also equip yourself with the tools to tackle more complex scenarios involving fractions and division. The ability to translate abstract mathematical concepts into tangible solutions is key to applying mathematics effectively in the real world. Remember, a strong foundation in fractions is essential for success in many academic and professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many 1/3 Are In 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.