How Many 2/5 Are In 1 1/2
News Co
Apr 28, 2025 · 5 min read
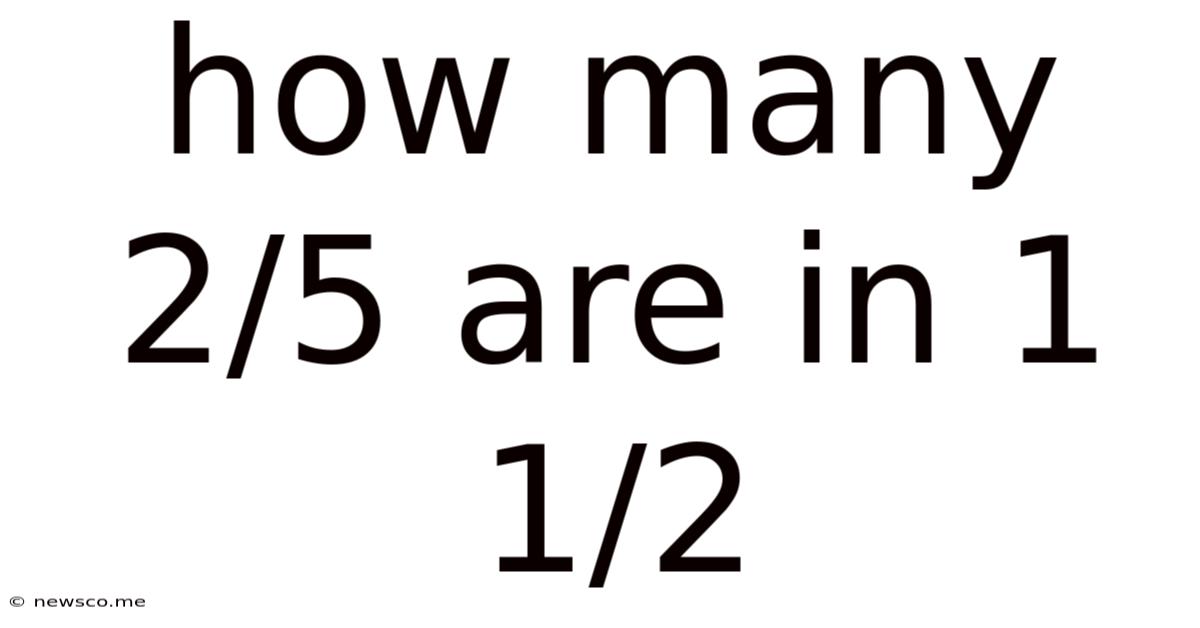
Table of Contents
How Many 2/5 Are in 1 1/2? A Comprehensive Guide to Fraction Division
This seemingly simple question – "How many 2/5 are in 1 1/2?" – opens the door to a deeper understanding of fraction division. While the answer itself is straightforward, the process of arriving at it, and the broader implications of understanding fraction division, are crucial for anyone aiming to master mathematics. This guide will delve into not just the solution, but also the underlying concepts, offering multiple approaches to tackle similar problems. We'll explore why understanding this is important and how it applies to everyday life and various fields.
Understanding the Problem: Fraction Division
The question, "How many 2/5 are in 1 1/2?", is essentially asking us to perform a division operation. We're trying to determine how many times the fraction 2/5 fits into the mixed number 1 1/2. This translates to the mathematical expression: (1 1/2) ÷ (2/5).
Converting Mixed Numbers to Improper Fractions
Before we dive into the division, it's crucial to convert the mixed number 1 1/2 into an improper fraction. A mixed number combines a whole number and a fraction (e.g., 1 1/2). An improper fraction has a numerator larger than or equal to its denominator (e.g., 3/2).
To convert 1 1/2 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator: 2 + 1 = 3
- Keep the same denominator: 2
Therefore, 1 1/2 is equivalent to 3/2.
Method 1: The Reciprocal Method
This is the most common method taught for dividing fractions. It involves inverting (finding the reciprocal of) the second fraction and then multiplying.
- Rewrite the problem: (3/2) ÷ (2/5)
- Invert the second fraction (the divisor): The reciprocal of 2/5 is 5/2.
- Change the division to multiplication: (3/2) * (5/2)
- Multiply the numerators and the denominators: (3 * 5) / (2 * 2) = 15/4
- Simplify the result (if possible): 15/4 can be converted to a mixed number: 3 3/4
Therefore, there are 3 3/4 of 2/5 in 1 1/2.
Method 2: Using Common Denominators
This method avoids the reciprocal step and relies on finding a common denominator for both fractions.
- Find a common denominator: The least common multiple (LCM) of 2 and 5 is 10.
- Convert both fractions to have the common denominator:
- 3/2 = (3 * 5) / (2 * 5) = 15/10
- 2/5 = (2 * 2) / (5 * 2) = 4/10
- Rewrite the division problem: (15/10) ÷ (4/10)
- Divide the numerators: 15 ÷ 4 = 3.75
- Alternatively, we can think of it as: 15/10 divided by 4/10 is the same as 15 divided by 4 because the "/10" cancels out. This leaves us with 3.75
- Convert to a fraction: 3.75 = 15/4 = 3 3/4
Again, we arrive at the same answer: 3 3/4.
Method 3: Visual Representation
While not always practical for complex fractions, visualizing the problem can be helpful for understanding the concept. Imagine you have a pie representing 1 1/2. Now, try to divide that pie into pieces of size 2/5. You'll find you can fit three full pieces (2/5) and a bit more, which corresponds to 3/4 of another piece (2/5).
This visual approach helps solidify the understanding of what fraction division truly represents.
The Importance of Mastering Fraction Division
Understanding fraction division is fundamental to various aspects of mathematics and beyond:
- Everyday Applications: Dividing recipes, calculating material quantities for DIY projects, sharing items fairly, and understanding proportions all involve fraction division.
- Higher-Level Mathematics: Fraction division forms the basis for more advanced topics like algebra, calculus, and trigonometry. A strong foundation in fractions is essential for success in these areas.
- Science and Engineering: Many scientific and engineering calculations rely heavily on fractions and the ability to perform operations on them accurately. From calculating ratios and proportions to solving equations involving fractions, this skill is indispensable.
- Financial Literacy: Managing budgets, understanding interest rates, calculating discounts, and interpreting financial reports all frequently involve working with fractions and percentages.
Solving Similar Problems: Practice and Application
To further solidify your understanding, let's tackle a few similar problems:
Problem 1: How many 3/8 are in 2 1/4?
- Convert 2 1/4 to an improper fraction: 9/4
- Divide: (9/4) ÷ (3/8) = (9/4) * (8/3) = 72/12 = 6 There are 6 of 3/8 in 2 1/4.
Problem 2: How many 1/3 are in 2/9?
- Divide: (2/9) ÷ (1/3) = (2/9) * (3/1) = 6/9 = 2/3 There are 2/3 of 1/3 in 2/9.
Problem 3: How many 5/6 are in 2 1/3?
- Convert 2 1/3 to an improper fraction: 7/3
- Divide: (7/3) ÷ (5/6) = (7/3) * (6/5) = 42/15 = 14/5 = 2 4/5 There are 2 4/5 of 5/6 in 2 1/3.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question of "How many 2/5 are in 1 1/2?" unveils the importance of understanding fraction division. This fundamental mathematical operation has far-reaching implications across numerous fields and everyday situations. By mastering various methods for solving fraction division problems, you build a strong mathematical foundation that will serve you well in your academic pursuits and beyond. Remember to practice regularly and explore different approaches to find the method that suits you best. The ability to confidently tackle fraction division is a key component of numerical fluency and a valuable skill for life.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many 2/5 Are In 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.