How Many 2 Digit Numbers Are There
News Co
Apr 05, 2025 · 5 min read
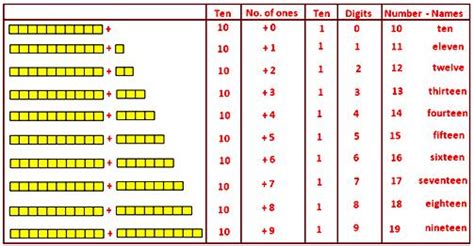
Table of Contents
How Many 2-Digit Numbers Are There? A Deep Dive into Counting Techniques
The seemingly simple question, "How many 2-digit numbers are there?" opens the door to a fascinating exploration of number systems, counting techniques, and even a touch of combinatorics. While the answer might seem immediately obvious to some, a deeper dive reveals valuable insights into mathematical principles that extend far beyond this specific problem. This article will not only answer the question definitively but also explore the underlying logic and demonstrate how this type of problem can be approached in various ways, building a strong foundation for more complex mathematical challenges.
Understanding the Nature of 2-Digit Numbers
Before we delve into the counting process, let's define what constitutes a 2-digit number. We're specifically interested in numbers that require two digits to represent them in the base-10 (decimal) system. This excludes single-digit numbers (0-9) and includes numbers ranging from 10 to 99. This seemingly small distinction is crucial for accurate counting.
The Importance of Place Value
The base-10 system, which we commonly use, relies on place value. Each digit in a number occupies a specific position, and its value depends on that position. In a 2-digit number, the leftmost digit represents the tens place, and the rightmost digit represents the ones place. For example, in the number 27, the 2 represents 20 (two tens) and the 7 represents 7 (seven ones).
Method 1: Direct Counting
The most straightforward approach to solving this problem is simply to count the numbers. We can start at 10 and continue counting up to 99. While feasible for this small range, this method becomes incredibly inefficient for larger ranges of numbers or more complex counting problems.
However, this method helps build an intuitive understanding of the problem. By counting manually, we can confirm the answer and gain a practical feel for the concept. Let's do it!
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20… and so on until 99.
While tedious, it reinforces that there are indeed a significant number of 2-digit numbers.
Method 2: Subtraction
A more elegant and efficient approach involves using subtraction. We know the smallest 2-digit number is 10 and the largest is 99. To find the total number of 2-digit numbers, we simply subtract the smallest from the largest and then add 1:
99 - 10 + 1 = 90
The addition of 1 is crucial because it includes both the starting and ending numbers in the count. This method is significantly faster and more scalable than direct counting.
Why Add 1?
The reason we add 1 is because we're counting inclusive of both the smallest and largest numbers. If we only subtracted (99 - 10 = 89), we would be missing one number in our count – the number 99 itself. This seemingly small detail is a common source of error in counting problems.
Method 3: Combinatorics (Permutations and Combinations)
For those familiar with combinatorics, this problem can also be solved using permutation and combination principles. Although this might seem overly complex for such a simple problem, it highlights the flexibility of mathematical tools and builds a strong foundation for handling more challenging counting scenarios.
In this case, we have two positions to fill: the tens place and the ones place.
- Tens place: We can fill this place with any digit from 1 to 9 (we exclude 0 because it would create a single-digit number). So we have 9 choices.
- Ones place: We can fill this place with any digit from 0 to 9. This gives us 10 choices.
To find the total number of possibilities, we multiply the number of choices for each place:
9 choices (tens place) * 10 choices (ones place) = 90
This confirms our previous result. This combinatorial approach becomes especially powerful when dealing with problems involving more digits or more restrictive conditions.
Extending the Concept: Numbers with More Digits
The techniques discussed above can be readily extended to count numbers with more digits. For instance, to find the number of 3-digit numbers:
- Direct Counting: Extremely impractical.
- Subtraction: 999 - 100 + 1 = 900
- Combinatorics: 9 (hundreds place) * 10 (tens place) * 10 (ones place) = 900
This demonstrates the scalability and efficiency of the subtraction and combinatorial methods.
Real-World Applications of Counting Techniques
Understanding how to count numbers efficiently is not just a theoretical exercise; it has significant real-world applications across numerous fields:
- Computer Science: Counting the number of possible states, permutations, or combinations is essential in algorithm design and analysis.
- Cryptography: Understanding the number of possible keys in an encryption system is critical for security.
- Probability and Statistics: Counting the number of favorable outcomes is fundamental in calculating probabilities.
- Data Analysis: Determining the size of data sets and performing calculations based on the number of data points is essential for data analysis.
- Finance: Calculating the number of possible investment strategies or portfolio combinations is vital in financial modeling.
Avoiding Common Pitfalls in Counting Problems
Several common pitfalls can lead to incorrect results when solving counting problems. Understanding these pitfalls is crucial for accuracy:
- Ignoring Inclusive/Exclusive Counting: Remember to consider whether your counting needs to be inclusive or exclusive of the endpoints. The "plus 1" is a frequent source of error.
- Incorrectly Applying Permutations/Combinations: Carefully consider whether order matters (permutations) or not (combinations). Using the incorrect method will lead to incorrect results.
- Overcounting or Undercounting: Double-check your counting method to ensure you're not accidentally counting some items twice or missing some.
- Not Clearly Defining the Problem: Before you begin, clearly define the parameters of the problem. Are you counting only integers? Are there any restrictions on the digits?
Conclusion: Beyond the Basics
The simple question of how many 2-digit numbers exist serves as a gateway to a rich understanding of fundamental mathematical concepts. While the answer – 90 – is straightforward, the various methods of arriving at that answer illuminate powerful problem-solving techniques applicable to a vast array of mathematical and real-world challenges. By understanding the underlying logic and avoiding common pitfalls, you can confidently tackle more complex counting problems and develop a strong foundation in mathematical reasoning. The seemingly simple act of counting opens up a world of possibilities in understanding and applying mathematical principles. The ability to count accurately and efficiently is a crucial skill in numerous disciplines, and mastering these techniques is a valuable asset for any learner.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many 2 Digit Numbers Are There . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.