How Many 5 8 Are In 1
News Co
May 07, 2025 · 5 min read
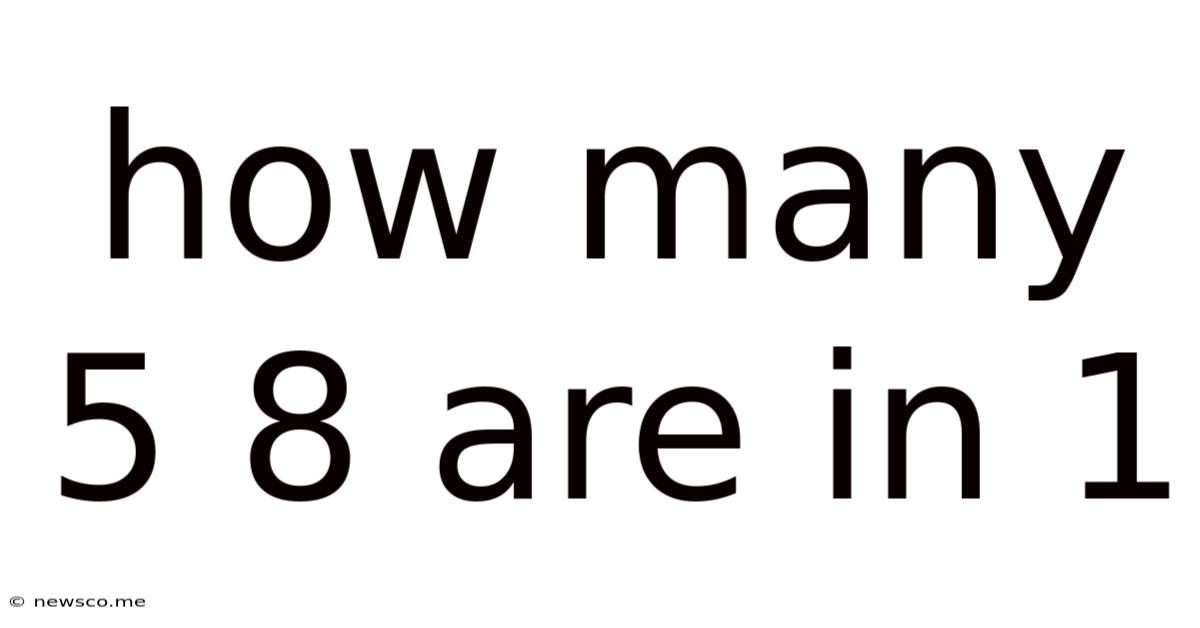
Table of Contents
How Many 5/8s Are in 1? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 5/8s are in 1?", opens the door to a fascinating exploration of fractions, division, and the fundamental principles of mathematics. While the answer might seem immediately obvious to some, understanding the why behind the answer is crucial for building a solid mathematical foundation. This article will delve into the intricacies of this problem, exploring various approaches to solving it and expanding upon the concepts involved. We'll also touch upon practical applications and explore how this type of problem applies to real-world scenarios.
Understanding Fractions: The Building Blocks
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the fraction 5/8, the numerator (5) tells us we have 5 parts, and the denominator (8) tells us the whole is divided into 8 equal parts.
Different Approaches to Solving the Problem
There are several ways to approach the problem of determining how many 5/8s are in 1. Let's explore three common methods:
Method 1: Using Division
The most straightforward method is to use division. We want to find out how many times 5/8 goes into 1. This can be expressed as a division problem:
1 ÷ (5/8)
To divide by a fraction, we multiply by its reciprocal (flip the fraction):
1 × (8/5) = 8/5
This gives us the answer as an improper fraction (8/5). To convert this to a mixed number (a whole number and a fraction), we perform the division:
8 ÷ 5 = 1 with a remainder of 3.
Therefore, there are 1 and 3/5 5/8s in 1.
Method 2: Visual Representation
A visual approach can make the concept more intuitive. Imagine a whole circle (representing 1). We divide this circle into 8 equal slices. Each slice represents 1/8 of the whole. A group of 5 slices represents 5/8.
To find how many 5/8s are in 1, we ask: how many groups of 5 slices can we make from 8 slices? We can make one full group (5 slices) with 3 slices remaining. This visually confirms our answer: 1 and 3/5.
Method 3: Using Equivalent Fractions
We can also solve this problem by finding an equivalent fraction for 1 with a denominator of 8. Since 8/8 = 1, we can rewrite the problem as:
(8/8) ÷ (5/8)
When dividing fractions with the same denominator, we can simply divide the numerators:
8 ÷ 5 = 8/5
This again gives us the improper fraction 8/5, which converts to the mixed number 1 and 3/5.
Expanding the Concept: Applications in Real-World Scenarios
The seemingly simple concept of determining how many 5/8s are in 1 has far-reaching applications in various real-world scenarios:
-
Measurement and Conversion: Imagine you're working with a recipe that requires 5/8 of a cup of flour, and you only have a 1-cup measuring cup. Understanding how many 5/8s are in 1 helps you accurately measure the required amount.
-
Resource Allocation: If you have a project that requires 1 unit of work, and each worker can complete 5/8 of a unit per day, you can determine how many workers you need to complete the project in a day.
-
Finance and Budgeting: Similar applications exist in finance, where you might be dealing with fractions of a stock or a budget. Understanding fraction manipulation is critical for accurate calculations.
-
Construction and Engineering: Precise measurements are vital in construction and engineering. Working with fractions is often unavoidable and this principle is used to ensure precision in layouts and materials usage.
-
Data Analysis: In data analysis and statistics, working with fractions and percentages is fundamental. Understanding the relationships between these concepts is essential for interpreting data accurately.
Beyond the Basics: Exploring More Complex Scenarios
While this article focuses on the specific problem of finding how many 5/8s are in 1, the underlying principles can be applied to more complex scenarios involving different fractions and whole numbers. The methods of division, visual representation, and equivalent fractions remain invaluable tools in tackling these more challenging problems.
Consider, for example, the problem of finding how many 3/7s are in 2. The same logic applies:
-
Division: 2 ÷ (3/7) = 2 × (7/3) = 14/3 = 4 and 2/3
-
Visual Representation: Imagine two whole circles divided into sevenths. You can count how many groups of 3 sevenths are in 14 sevenths.
-
Equivalent Fractions: Express 2 as a fraction with a denominator of 7 (14/7), then divide by 3/7: (14/7) ÷ (3/7) = 14/3 = 4 and 2/3
Mastering Fractions: A Crucial Skill
Understanding fractions and the ability to perform operations with them is a fundamental skill in mathematics. This simple question about how many 5/8s are in 1 serves as a gateway to a deeper understanding of mathematical concepts that have broad applications in various fields. By mastering these concepts, you equip yourself with invaluable tools for problem-solving and critical thinking. The more you practice, the more comfortable and confident you'll become in tackling these types of problems.
Remember, practice is key to mastering fractions. Try solving similar problems with different fractions to reinforce your understanding. Explore additional resources and online tools to further enhance your skills. With dedication and practice, you'll become proficient in working with fractions and confidently apply these concepts in various real-world situations.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many 5 8 Are In 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.