How Many Groups Of 3/4 Are In 4 1/2
News Co
Apr 28, 2025 · 5 min read
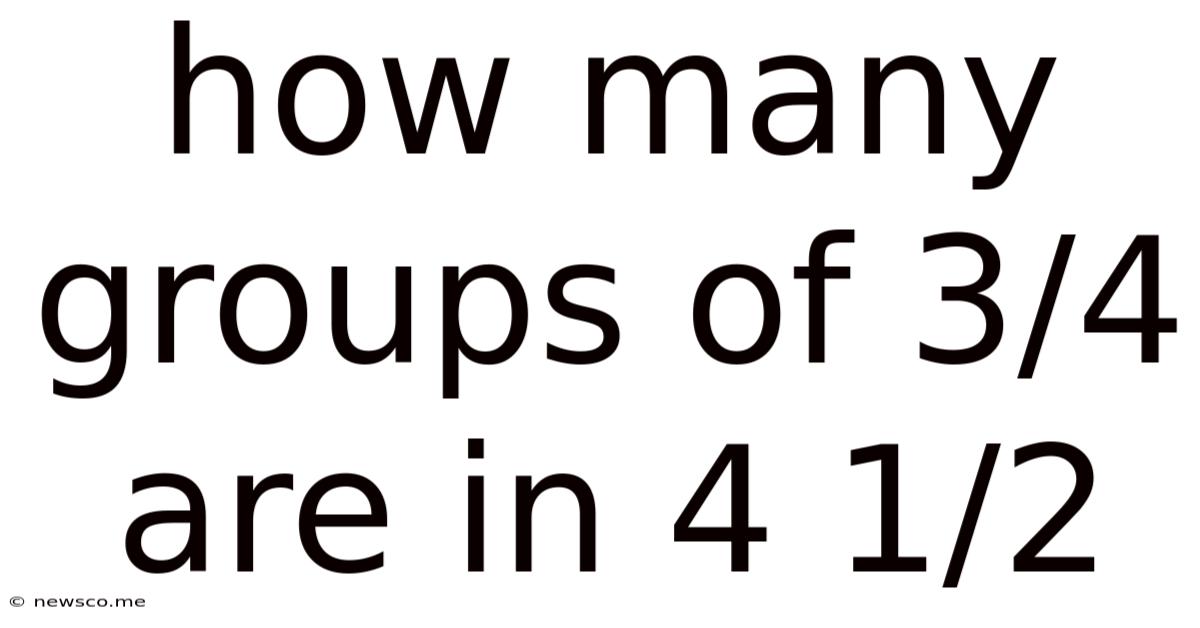
Table of Contents
How Many Groups of 3/4 Are in 4 1/2? A Comprehensive Guide to Fraction Division
Understanding fraction division is crucial for various mathematical applications, from simple baking recipes to complex engineering calculations. This comprehensive guide will walk you through solving the problem "How many groups of 3/4 are in 4 1/2?" step-by-step, exploring different methods and providing valuable insights into the underlying concepts. We'll delve into the intricacies of fraction division, explaining why specific methods work and offering practical tips to improve your understanding and problem-solving skills.
Understanding the Problem: A Visual Approach
Before diving into the calculations, let's visualize the problem. Imagine you have 4 1/2 pizzas, and each serving (group) is 3/4 of a pizza. The question is: how many servings can you get from the available pizzas?
This visualization helps to understand that we're essentially dividing a larger quantity (4 1/2) into smaller units (3/4). This is precisely what fraction division is all about.
Method 1: Converting Mixed Numbers to Improper Fractions
This is arguably the most common and efficient method for dividing fractions. The first step is to convert both the mixed numbers (4 1/2 and 3/4) into improper fractions.
Converting 4 1/2 to an Improper Fraction
A mixed number represents a whole number and a fraction. To convert it to an improper fraction (where the numerator is larger than the denominator), we follow these steps:
- Multiply the whole number by the denominator: 4 * 2 = 8
- Add the numerator: 8 + 1 = 9
- Keep the same denominator: 2
Therefore, 4 1/2 is equal to 9/2.
Converting 3/4 to an Improper Fraction
Since 3/4 is already an improper fraction (or at least a simple fraction), no conversion is needed. It remains 3/4.
Performing the Division
Now we can perform the division: (9/2) ÷ (3/4). Dividing fractions involves inverting (flipping) the second fraction (the divisor) and then multiplying:
(9/2) * (4/3) = (9 * 4) / (2 * 3) = 36 / 6 = 6
Therefore, there are 6 groups of 3/4 in 4 1/2.
Method 2: Using Decimal Equivalents
Another approach involves converting the fractions to decimals and then performing the division.
Converting Fractions to Decimals
- 4 1/2 = 4.5
- 3/4 = 0.75
Performing the Decimal Division
Now, we divide 4.5 by 0.75:
4.5 ÷ 0.75 = 6
Again, we arrive at the answer of 6 groups. This method provides an alternative perspective and can be helpful for those more comfortable with decimal calculations.
Method 3: A Visual, Real-World Approach with Diagrams
Let's tackle this problem visually. Imagine dividing a rectangular area representing 4 1/2 pizzas into sections of 3/4 pizza each.
First, we have four whole pizzas, and each can be easily divided into 3/4 sections. That’s four pizzas divided into (4 * 3/4) = 3 servings each, for a total of 12 servings. We can visually divide each pizza into 4 pieces representing 1/4 each. Since a serving is 3/4, each pizza yields 1 full serving (3 pieces out of 4).
Now, let's tackle the half-pizza. We know a whole pizza has 4 quarters (1/4 slices). Therefore, half a pizza is 2 quarters (2/4). We can see that 2/4 (or 1/2) is equal to 2/3 of a 3/4 serving. In other words, half a pizza doesn't quite make a full serving.
However, this is where things get a little tricky. If we consider the fraction of 1/2 a pizza, this is equivalent to 2/4. To complete one serving (3/4), we would need 1/4 more. This 1/4 pizza cannot form a whole serving (3/4) on its own. Hence, we can't get another full group.
This visual approach highlights the importance of precise fraction manipulation, reinforcing the effectiveness of the improper fraction method. The visual confirmation supports the answer derived through algebraic methods.
Understanding the Concept of Fraction Division
The fundamental concept underlying this problem, and fraction division in general, is finding how many times a smaller fraction fits into a larger fraction. It's about determining the number of groups or parts. The core idea is to invert and multiply, a technique that effectively transforms the division problem into a multiplication problem.
Practical Applications and Extensions
This type of problem isn't confined to pizzas. It finds applications in numerous areas:
- Cooking: Scaling recipes up or down.
- Sewing: Calculating fabric requirements.
- Construction: Determining material quantities.
- Finance: Calculating proportions and shares.
The ability to confidently divide fractions is a cornerstone of many practical applications.
Troubleshooting Common Errors
When working with fractions, certain common mistakes can lead to inaccurate results. Here are some points to watch out for:
- Improper Fraction Conversion: Ensure you correctly convert mixed numbers to improper fractions before performing any calculations. An error here will cascade through the entire problem.
- Inverting and Multiplying: Remember to invert only the second fraction (the divisor) before multiplying. Inverting both fractions will lead to an incorrect answer.
- Simplifying Fractions: Always simplify your final answer to its lowest terms. This makes the result more easily understandable and interpretable.
Beyond the Basics: Exploring More Complex Fraction Division Problems
While this example focused on relatively straightforward fractions, the same principles apply to more complex problems involving larger numbers or more intricate fractions. The key is to maintain a methodical approach, focusing on accurate conversions and careful calculations. Practice is key to mastering fraction division.
Conclusion: Mastering Fraction Division for Success
Understanding how to divide fractions is a fundamental skill with wide-ranging applications. This comprehensive guide explored various methods for solving the problem, "How many groups of 3/4 are in 4 1/2?", demonstrating the importance of converting to improper fractions and the power of visualization. By understanding these methods and avoiding common pitfalls, you can confidently tackle similar fraction division problems and apply this valuable skill to various real-world situations. Remember, consistent practice and a clear understanding of the underlying principles will lead to mastery.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Groups Of 3/4 Are In 4 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.