How Many Lines Of Symmetry Does Octagon Have
News Co
Apr 08, 2025 · 5 min read
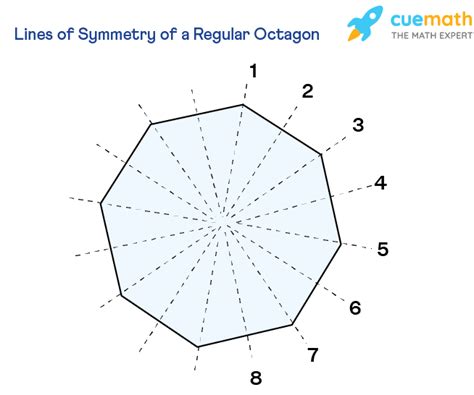
Table of Contents
How Many Lines of Symmetry Does an Octagon Have? A Comprehensive Guide
Symmetry, a fundamental concept in geometry and art, refers to the harmonious and balanced distribution of elements within a shape or figure. Understanding lines of symmetry is crucial in various fields, from mathematics and design to architecture and nature. This comprehensive guide delves into the fascinating world of symmetry, focusing specifically on the octagon and its lines of symmetry. We'll explore different types of octagons, how to identify lines of symmetry, and the mathematical principles behind them.
What is a Line of Symmetry?
Before we dive into the intricacies of octagons, let's define the core concept: a line of symmetry. A line of symmetry, also known as a line of reflection, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along this line, the two halves would perfectly overlap. A shape can have multiple lines of symmetry, or none at all.
Types of Octagons
Octagons are eight-sided polygons. However, not all octagons are created equal. Their lines of symmetry depend heavily on their specific characteristics. We can categorize octagons into two main types relevant to our discussion of symmetry:
1. Regular Octagon
A regular octagon is a special type of octagon where all eight sides are equal in length, and all eight interior angles are equal (each measuring 135 degrees). This regularity directly impacts the number of lines of symmetry it possesses.
2. Irregular Octagon
An irregular octagon is any octagon that doesn't meet the criteria of a regular octagon. Its sides and angles can vary in length and measure. This irregularity significantly affects the number and types of lines of symmetry it may (or may not) have.
Lines of Symmetry in a Regular Octagon
The beauty of a regular octagon lies in its high degree of symmetry. It exhibits a remarkable number of lines of symmetry. Let's explore them systematically:
1. Lines of Symmetry Through Opposite Vertices
A regular octagon has four lines of symmetry that pass through opposite vertices (corners). Imagine drawing a line connecting two vertices that are directly across from each other. This line will divide the octagon perfectly into two mirror-image halves. Since there are four pairs of opposite vertices, there are four lines of symmetry of this type.
2. Lines of Symmetry Through Midpoints of Opposite Sides
In addition to the lines connecting opposite vertices, a regular octagon also possesses four lines of symmetry that pass through the midpoints of opposite sides. These lines bisect the octagon, creating two congruent halves. Because there are four pairs of opposite sides, there are four lines of symmetry of this kind.
Total Lines of Symmetry in a Regular Octagon
Combining the lines of symmetry through opposite vertices and the lines through midpoints of opposite sides, a regular octagon has a total of eight lines of symmetry. This reflects its inherent balanced and harmonious structure.
Lines of Symmetry in an Irregular Octagon
The story is quite different for irregular octagons. The lack of consistent side lengths and angles drastically reduces the possibilities of lines of symmetry. An irregular octagon may have:
- Zero lines of symmetry: This is the most common scenario for irregular octagons. The asymmetrical arrangement of sides and angles prevents any line from dividing it into perfectly mirrored halves.
- One or more lines of symmetry: In rare cases, an irregular octagon might possess one or more lines of symmetry, but this is entirely dependent on the specific dimensions and arrangement of its sides and angles. There is no fixed number, and each case requires individual analysis.
Visualizing Lines of Symmetry
To better understand the lines of symmetry in an octagon, consider the following visualizations:
- Folding: Imagine cutting out a paper octagon. Try folding it along different lines. If the two halves perfectly overlap, you've found a line of symmetry.
- Mirror Image: Place a mirror along a potential line of symmetry. If the reflection in the mirror exactly matches the other half of the octagon, you've identified a line of symmetry.
- Geometric Software: Use dynamic geometry software (like GeoGebra) to create octagons and explore different lines to visually confirm lines of symmetry.
Mathematical Proof for Regular Octagon's Symmetry
The existence of eight lines of symmetry in a regular octagon can be rigorously proven using mathematical principles of rotational symmetry and reflectional symmetry.
A regular octagon has rotational symmetry of order 8. This means it can be rotated around its center by multiples of 45 degrees (360°/8 = 45°) and still appear identical. Each rotational symmetry corresponds to a line of reflectional symmetry.
Furthermore, a regular polygon with 'n' sides always has 'n' lines of reflectional symmetry if 'n' is even. Since an octagon has 8 sides (an even number), it must have 8 lines of reflectional symmetry. Half of these lines pass through opposite vertices, and the other half pass through the midpoints of opposite sides.
Applications of Symmetry in Real Life
Understanding lines of symmetry isn't just an academic exercise. Symmetry plays a significant role in many aspects of our lives:
- Art and Design: Artists and designers utilize symmetry to create aesthetically pleasing and balanced compositions. From architecture to logos and patterns, symmetry is a fundamental design principle.
- Nature: Many natural formations exhibit symmetry, such as snowflakes, flowers, and even the human body (although not perfectly symmetrical).
- Engineering and Construction: Symmetrical designs are often preferred in engineering and construction as they provide structural stability and balance.
- Mathematics and Physics: Symmetry is a crucial concept in many areas of mathematics and physics, with profound implications for understanding the universe.
Conclusion
The number of lines of symmetry in an octagon is directly related to its regularity. A regular octagon boasts eight lines of symmetry – four through opposite vertices and four through midpoints of opposite sides. Irregular octagons, however, can have fewer lines of symmetry or none at all. Understanding the concept of symmetry and its application to different shapes like octagons is fundamental in various fields, enriching our understanding of geometry, design, and the natural world around us. By exploring this topic further, you can deepen your appreciation for the mathematical beauty inherent in seemingly simple shapes. The exploration of symmetry continues to fascinate mathematicians, artists, and scientists alike, highlighting the power of simple concepts to unlock complex understandings. The world of symmetry is vast and ever-expanding, offering endless opportunities for discovery and creative exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does Octagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.