How Many Lines Of Symmetry Has A Rectangle
News Co
Apr 04, 2025 · 6 min read
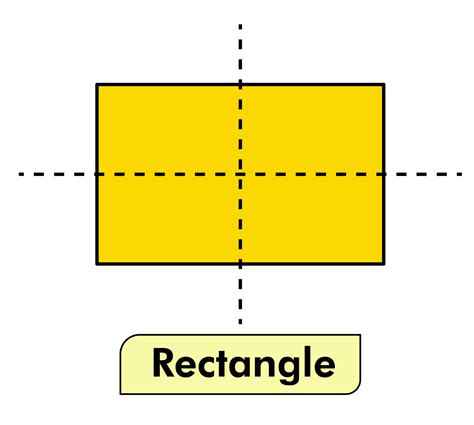
Table of Contents
How Many Lines of Symmetry Does a Rectangle Have? A Comprehensive Exploration
Symmetry, a concept fundamental to geometry and art, refers to a balanced and proportionate arrangement of parts. Understanding lines of symmetry is crucial for analyzing shapes and solving geometric problems. This article delves into the fascinating world of symmetry, focusing specifically on the number of lines of symmetry a rectangle possesses. We'll explore the definition of symmetry, different types of symmetry, and then dissect the specific case of rectangles, explaining why they have the number of lines of symmetry they do. We will also examine related shapes and their symmetry properties for a richer understanding.
Understanding Lines of Symmetry
A line of symmetry, also known as a line of reflection or axis of symmetry, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, both halves would perfectly overlap. This means every point on one half of the shape has a corresponding point on the other half at an equal distance from the line of symmetry.
There are several types of symmetry:
- Reflectional Symmetry (Line Symmetry): This is the type of symmetry we're primarily concerned with here. It involves a line of symmetry, as described above.
- Rotational Symmetry: This type of symmetry involves rotating the shape around a central point. If the shape looks identical after a rotation of less than 360 degrees, it possesses rotational symmetry.
- Translational Symmetry: This involves sliding the shape along a line without changing its orientation.
- Point Symmetry: This exists when a shape can be rotated 180 degrees about a central point and still look the same.
Exploring the Rectangle and its Lines of Symmetry
A rectangle is a quadrilateral (a four-sided polygon) with four right angles (90-degree angles). Opposite sides of a rectangle are parallel and equal in length. This specific set of properties directly impacts the number of lines of symmetry a rectangle possesses.
To determine the number of lines of symmetry in a rectangle, let's consider the properties mentioned above:
-
Equal and Parallel Opposite Sides: Because opposite sides are equal and parallel, a line drawn directly connecting the midpoints of opposite sides will act as a line of symmetry. Folding the rectangle along this line would perfectly overlap the two halves. Since there are two pairs of opposite sides, we have two such lines of symmetry.
-
Right Angles: The four 90-degree angles ensure that the shape is balanced and creates the possibility for additional lines of symmetry. A line drawn through the diagonals of the rectangle will not create two mirrored halves.
Therefore, a rectangle has exactly two lines of symmetry. These lines are perpendicular to each other and pass through the center of the rectangle. They run parallel to the sides of the rectangle and bisect the opposite sides.
Visualizing the Lines of Symmetry
Imagine a rectangle. Now, draw a line connecting the midpoints of the top and bottom sides. This is one line of symmetry. Next, draw a line connecting the midpoints of the left and right sides. This is the second line of symmetry. You will observe that these two lines intersect at the center of the rectangle, creating four congruent quadrants.
Distinguishing Rectangles from Squares
It's crucial to differentiate rectangles from squares. While a square is a special type of rectangle (all its sides are equal), it possesses additional lines of symmetry. A square has four lines of symmetry: the two lines parallel to its sides, like a rectangle, and two additional lines that connect opposite vertices (corners). These diagonal lines also bisect the right angles, resulting in perfect mirror images.
Mathematical Proof of Two Lines of Symmetry in a Rectangle
We can mathematically prove that a rectangle has only two lines of symmetry. Let's consider a rectangle with vertices at coordinates (0, b), (a, b), (a, 0), and (0, 0), where 'a' and 'b' represent the lengths of the sides.
A line of symmetry must divide the rectangle into two congruent halves. The only lines satisfying this condition are the lines passing through the midpoints of opposite sides. These lines can be represented by equations:
- x = a/2: This line passes through the midpoints of the vertical sides.
- y = b/2: This line passes through the midpoints of the horizontal sides.
Any other line will not divide the rectangle into two congruent halves that are mirror images of each other. Therefore, a rectangle has only two lines of symmetry.
Applications of Symmetry in Real Life
Understanding lines of symmetry extends beyond abstract mathematical concepts. Its applications are widespread across various fields:
- Architecture and Design: Architects and designers utilize symmetry to create visually appealing and balanced structures. Buildings, bridges, and furniture often incorporate symmetrical designs.
- Art: Artists throughout history have employed symmetry to enhance the aesthetic appeal of their works. Many paintings, sculptures, and other artistic creations demonstrate a strong sense of symmetry.
- Nature: Symmetry is prevalent in nature. Many natural objects, like snowflakes, butterflies, and flowers, exhibit remarkable symmetry.
- Engineering: Symmetry plays a crucial role in engineering design, ensuring stability and balance in structures and machines.
Beyond Rectangles: Symmetry in Other Shapes
Let's briefly explore the lines of symmetry in other common shapes:
- Square: As mentioned earlier, a square has four lines of symmetry: two parallel to its sides and two along its diagonals.
- Circle: A circle has an infinite number of lines of symmetry. Any line passing through the center of the circle is a line of symmetry.
- Equilateral Triangle: An equilateral triangle (all sides equal) has three lines of symmetry, each line passing through a vertex and the midpoint of the opposite side.
- Isosceles Triangle: An isosceles triangle (two equal sides) has one line of symmetry, which passes through the vertex formed by the two equal sides and bisects the unequal side.
- Regular Pentagon: A regular pentagon (five equal sides) has five lines of symmetry, each line connecting a vertex to the midpoint of the opposite side.
Conclusion: The Definitive Answer
In conclusion, a rectangle possesses precisely two lines of symmetry. These lines bisect the opposite sides and are perpendicular to each other. Understanding the concept of lines of symmetry is not only essential for grasping fundamental geometric principles but also for appreciating the beauty and balance found in shapes all around us, both in the natural world and in human creations. This knowledge extends to other geometric figures, expanding your understanding of symmetry's role in mathematics, art, design, and more. The careful analysis of lines of symmetry helps us understand the inherent properties and characteristics of geometric shapes, making it a cornerstone of geometric study.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Has A Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.