How Many Lines Of Symmetry In Hexagon
News Co
Apr 06, 2025 · 6 min read
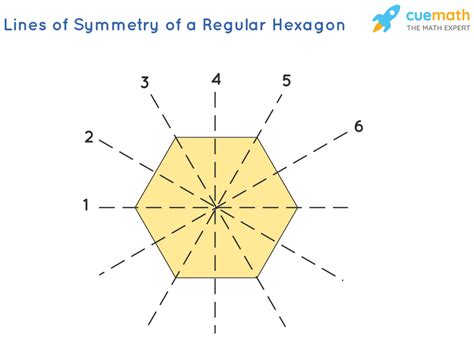
Table of Contents
How Many Lines of Symmetry Does a Hexagon Have? A Deep Dive into Geometry
Symmetry, a fundamental concept in mathematics and art, captivates us with its inherent beauty and order. Understanding symmetry, especially in geometric shapes, is crucial for various fields, from art and design to engineering and crystallography. This article delves into the fascinating world of symmetry, specifically focusing on the number of lines of symmetry in a hexagon, exploring different types of hexagons and the mathematical principles behind their symmetrical properties.
Understanding Lines of Symmetry
Before we embark on our hexagon exploration, let's establish a clear understanding of what a line of symmetry is. A line of symmetry, also known as a line of reflection, is a line that divides a shape into two identical halves that are mirror images of each other. When you fold the shape along the line of symmetry, the two halves perfectly overlap. Not all shapes possess lines of symmetry; some might have none, while others can have multiple.
Types of Hexagons: Regular vs. Irregular
Hexagons, six-sided polygons, come in various forms. The key distinction lies between regular hexagons and irregular hexagons.
Regular Hexagons: The Symmetrical Stars
A regular hexagon is a hexagon with all sides equal in length and all interior angles equal (each angle measuring 120 degrees). This uniformity is the key to its remarkable symmetry. It's a highly symmetrical shape, exhibiting a significant number of lines of symmetry.
Irregular Hexagons: A World of Asymmetry
Irregular hexagons, on the other hand, lack this uniformity. Their sides and angles can vary significantly, resulting in a less symmetrical structure. The number of lines of symmetry in an irregular hexagon can range from zero to a maximum of three, depending on the specific arrangement of its sides and angles. It's important to note that many irregular hexagons will possess no lines of symmetry at all.
Lines of Symmetry in a Regular Hexagon: The Complete Picture
Now, let's focus on the star of our show – the regular hexagon. Its symmetrical nature leads to a substantial number of lines of symmetry. A regular hexagon possesses six lines of symmetry.
These lines can be categorized into two types:
1. Lines of Symmetry through Opposite Vertices
Three lines of symmetry pass through opposite vertices (corners) of the hexagon. These lines divide the hexagon into two identical, mirror-image trapezoids. Imagine drawing a line from one corner to the opposite corner – that's a line of symmetry. Since there are three pairs of opposite vertices in a hexagon, there are three lines of this type.
2. Lines of Symmetry through Midpoints of Opposite Sides
The other three lines of symmetry pass through the midpoints of opposite sides. These lines divide the hexagon into two identical, mirror-image quadrilaterals (specifically, parallelograms). Imagine drawing a line connecting the midpoint of one side to the midpoint of the opposite side – that's another line of symmetry. Again, with three pairs of opposite sides, you get three lines of this type.
Visualizing the Lines of Symmetry: A Practical Approach
The best way to understand the lines of symmetry in a regular hexagon is to visualize them. Try drawing a regular hexagon yourself and then carefully draw lines connecting:
- Opposite vertices: You'll find three lines.
- Midpoints of opposite sides: You'll find another three lines.
This visual exercise will solidify your understanding of the six lines of symmetry present in a regular hexagon.
Mathematical Proof and Rotational Symmetry
The existence of six lines of symmetry in a regular hexagon can also be proven mathematically. The high degree of symmetry in a regular hexagon is not limited to lines of symmetry; it also exhibits rotational symmetry. A regular hexagon has rotational symmetry of order 6, meaning it can be rotated six times (by 60 degrees each time) about its center and still look the same. This rotational symmetry is intrinsically linked to its lines of symmetry.
Applications of Hexagonal Symmetry
The symmetrical properties of hexagons are not merely an abstract mathematical concept; they have practical applications across various fields:
-
Honeycomb Structure: Bees use hexagonal cells in their honeycombs because this shape allows for the maximum storage space with minimal material usage. The inherent symmetry of the hexagon optimizes the structure’s efficiency.
-
Architecture and Design: Hexagons are frequently used in architecture and design due to their visual appeal and structural strength. The symmetrical nature lends itself to creating aesthetically pleasing and stable structures.
-
Engineering: Hexagonal patterns can be found in various engineering applications, from tiling to geodesic domes, leveraging the strength and stability offered by the symmetrical arrangement.
-
Crystallography: Many crystalline structures exhibit hexagonal symmetry, reflecting the underlying atomic arrangements. Understanding hexagonal symmetry is crucial for analyzing and predicting the properties of these materials.
Distinguishing Regular from Irregular Hexagons: A Key Consideration
It's crucial to remember that the six lines of symmetry are unique to regular hexagons. As soon as you deviate from the equal sides and equal angles, the symmetry is altered. An irregular hexagon might have fewer lines of symmetry (or none at all). The number of lines of symmetry decreases drastically as the regularity of the hexagon is compromised.
Beyond Lines of Symmetry: Exploring Other Symmetrical Properties
While lines of symmetry are a prominent feature of regular hexagons, other symmetrical properties further enhance their unique characteristics. Understanding these properties provides a deeper appreciation of the hexagon's geometrical elegance.
Advanced Concepts: Symmetry Groups and Mathematical Representations
For those interested in delving deeper, the concept of symmetry groups provides a formal mathematical framework for understanding and classifying symmetrical objects. The symmetry group of a regular hexagon, denoted as D6, encompasses all the possible symmetries (reflections and rotations) of the hexagon.
Conclusion: The Enduring Appeal of Hexagonal Symmetry
The number of lines of symmetry in a hexagon, particularly a regular hexagon, highlights the beauty and order inherent in geometrical shapes. This seemingly simple question opens the door to a deeper exploration of symmetry, its mathematical underpinnings, and its diverse applications across numerous fields. Whether you are an artist, an engineer, a mathematician, or simply a curious individual, understanding hexagonal symmetry offers a rewarding glimpse into the elegance and power of geometrical principles. The six lines of symmetry in a regular hexagon are not just a numerical fact; they are a testament to the fundamental principles of balance, harmony, and order that govern the world around us. This knowledge empowers us to appreciate the intricate beauty of the seemingly simple and to appreciate the connections between mathematics, art, and the world we inhabit.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry In Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.