How Many Lines Of Symmetry In Rectangle
News Co
Apr 15, 2025 · 5 min read
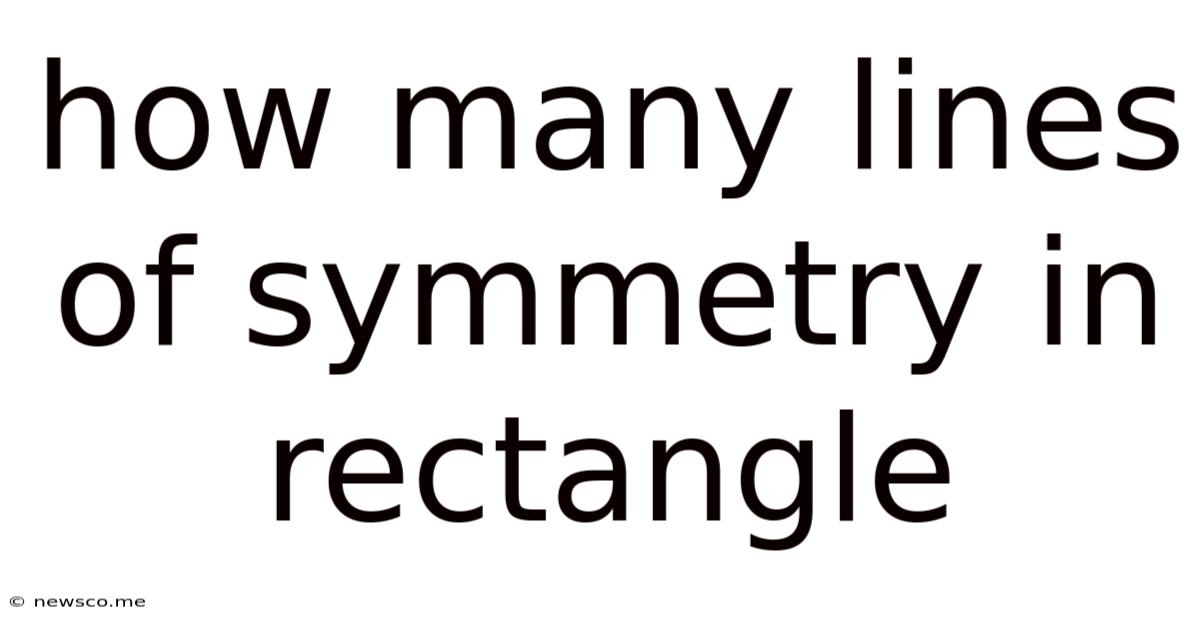
Table of Contents
How Many Lines of Symmetry Does a Rectangle Have? A Comprehensive Exploration
Symmetry, a fundamental concept in mathematics and geometry, refers to a balanced and proportionate arrangement of parts. Understanding lines of symmetry, also known as axes of symmetry, is crucial for grasping various geometric properties and applications. This article delves deep into the question: how many lines of symmetry does a rectangle possess? We'll explore the definition of symmetry, different types of quadrilaterals, and ultimately determine the number of lines of symmetry in a rectangle, along with practical examples and related concepts.
Understanding Lines of Symmetry
A line of symmetry, or axis of symmetry, is an imaginary line that divides a shape into two identical halves. If you were to fold the shape along this line, both halves would perfectly overlap. This mirroring effect is a key characteristic of symmetrical shapes. Shapes can have multiple lines of symmetry, or none at all. The number of lines of symmetry depends on the shape's regularity and its specific geometric properties.
Defining Symmetry in Geometry
Symmetry isn't just about visual appeal; it's a precise mathematical concept. In geometry, we specifically define lines of symmetry based on reflectional symmetry. This means that if you reflect a shape across the line of symmetry, the resulting image is identical to the original shape. This reflection preserves distances and angles, ensuring the two halves are congruent.
Types of Quadrilaterals and Their Symmetry
To understand the symmetry of a rectangle, we need to consider it within the broader context of quadrilaterals. Quadrilaterals are polygons with four sides. Different types of quadrilaterals exhibit varying degrees of symmetry:
1. Square:
The square boasts the highest level of symmetry among quadrilaterals. It possesses four lines of symmetry: two diagonals and two lines passing through the midpoints of opposite sides.
2. Rectangle:
Rectangles, including squares (which are special rectangles), exhibit a specific type of symmetry. They are characterized by having opposite sides that are equal and parallel.
3. Rhombus:
A rhombus has two lines of symmetry, both passing through opposite vertices. These lines bisect the angles at the vertices.
4. Parallelogram:
A parallelogram, unlike a rectangle or rhombus, generally has no lines of symmetry. However, a special type of parallelogram, a rectangle, does possess lines of symmetry.
5. Trapezoid:
Trapezoids generally have no lines of symmetry. An isosceles trapezoid, however, with two equal sides, can have one line of symmetry.
Determining the Lines of Symmetry in a Rectangle
Now, let's focus on the rectangle. A rectangle is a quadrilateral with four right angles and opposite sides equal in length. To determine its lines of symmetry, we consider the following:
-
Vertical Line of Symmetry: Imagine a line drawn vertically through the center of the rectangle, dividing it into two identical left and right halves. This is a line of symmetry.
-
Horizontal Line of Symmetry: Similarly, a horizontal line drawn through the center of the rectangle, dividing it into two identical top and bottom halves, also represents a line of symmetry.
Therefore, a rectangle has two lines of symmetry. These lines are perpendicular bisectors of each other and intersect at the center of the rectangle.
Squares: A Special Case of Rectangles
It's important to remember that a square is a special type of rectangle where all sides are equal in length. This additional property adds to its symmetry. While a rectangle has two lines of symmetry, a square, being a rectangle with equal sides, has four lines of symmetry. This is because the diagonals of a square also act as lines of symmetry.
Visualizing the Lines of Symmetry
To better visualize the lines of symmetry in a rectangle, consider drawing a rectangle on a piece of paper. Then, fold the paper along the vertical line passing through the midpoint of the opposite sides. The two halves should perfectly overlap. Repeat this process with a horizontal line, and again, the halves will perfectly overlap, confirming the existence of two lines of symmetry.
Applications of Symmetry in Real Life
The concept of symmetry is not just an abstract mathematical concept; it's prevalent in many aspects of our lives. Understanding lines of symmetry has practical applications in various fields:
-
Architecture and Design: Symmetrical designs are visually appealing and create a sense of balance and harmony in buildings, furniture, and other structures. Many architectural masterpieces utilize symmetry effectively.
-
Art and Nature: Symmetry is a recurring theme in art and nature. From paintings and sculptures to the intricate patterns found in snowflakes and flowers, symmetry plays a significant role in aesthetics.
-
Engineering and Technology: Symmetrical designs are crucial in engineering for stability and efficiency. Symmetrical components are often easier to manufacture and maintain.
-
Logo Design: Many company logos leverage symmetry for memorability and visual impact. A symmetrical logo is more easily recognizable and creates a stronger brand identity.
Beyond Lines of Symmetry: Rotational Symmetry
While this article focuses on lines of symmetry, it's important to mention rotational symmetry. Rotational symmetry occurs when a shape can be rotated about a central point and still appear unchanged. A rectangle possesses rotational symmetry of order 2, meaning it looks the same after a 180-degree rotation about its center. A square, on the other hand, exhibits rotational symmetry of order 4, looking identical after 90-degree, 180-degree, and 270-degree rotations.
Conclusion: The Two Lines of Symmetry in a Rectangle
In conclusion, a rectangle possesses two lines of symmetry: one vertical and one horizontal, both passing through the center of the rectangle. This characteristic distinguishes it from other quadrilaterals, like squares (which have four), rhombuses (which have two), and parallelograms (which typically have none). Understanding lines of symmetry and their application is fundamental to comprehending geometric properties and their diverse real-world applications, from architectural marvels to the elegance of nature's designs. The concept of symmetry is pervasive and holds a profound significance across many disciplines. The simple rectangle, with its two lines of symmetry, serves as a foundational example in exploring this vital geometric concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry In Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.