How Many Pairs Of Parallel Sides Does A Rectangle Have
News Co
Mar 18, 2025 · 5 min read
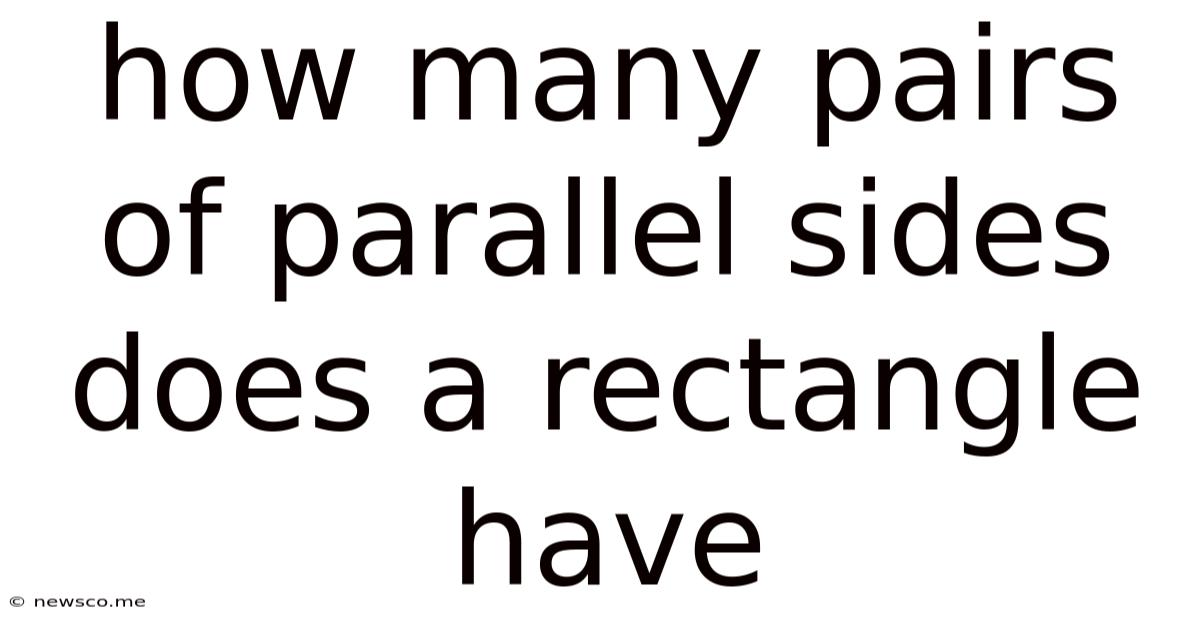
Table of Contents
How Many Pairs of Parallel Sides Does a Rectangle Have? A Deep Dive into Geometric Properties
The seemingly simple question, "How many pairs of parallel sides does a rectangle have?" opens a door to a fascinating exploration of geometry, specifically the properties of quadrilaterals and, more narrowly, rectangles. While the answer itself is straightforward, understanding why a rectangle possesses these parallel sides requires delving into the fundamental definitions and characteristics that define this fundamental geometric shape. This article will not only answer the question definitively but will also explore related concepts, providing a comprehensive understanding of rectangles and their place within the broader world of geometry.
Understanding Rectangles: A Definition
Before we delve into the number of parallel sides, let's establish a clear definition of a rectangle. A rectangle is a type of quadrilateral—a four-sided polygon—characterized by the following properties:
- Four right angles: Each of the four interior angles measures exactly 90 degrees. This is a crucial defining characteristic.
- Opposite sides are equal and parallel: This is where the answer to our main question lies. The opposite sides are not just equal in length; they are also parallel to each other. This parallelism is fundamental to the rectangle's properties.
- Two pairs of parallel sides: This is a direct consequence of the previous point. There are two distinct pairs of parallel sides.
The Significance of Parallelism in Rectangles
The parallelism of a rectangle's sides is not merely a descriptive feature; it's the foundation of many of its properties and applications. This parallelism ensures that:
- Diagonals bisect each other: The diagonals of a rectangle—lines connecting opposite vertices—intersect at their midpoints. This bisecting property is a direct result of the parallel and equal sides.
- Area calculation is straightforward: The area of a rectangle is simply the product of its length and width (Area = length x width). This simple formula relies heavily on the fact that the sides are parallel and perpendicular to each other.
- Stability and Construction: The parallel sides contribute to the structural stability of rectangular shapes. This makes rectangles ideal for building construction, furniture design, and many other applications where stability is essential.
Exploring the Number of Parallel Sides: A Visual Approach
Let's visualize a rectangle. Imagine a simple rectangle ABCD, where A, B, C, and D are the vertices. We can easily identify the parallel sides:
- AB is parallel to CD: These are one pair of parallel sides.
- BC is parallel to AD: These are the second pair of parallel sides.
Therefore, a rectangle has two pairs of parallel sides. This is not a coincidence; it's directly linked to the fundamental definition of a rectangle.
Differentiating Rectangles from Other Quadrilaterals
It's important to distinguish rectangles from other quadrilaterals to understand the unique significance of its parallel sides.
Rectangles vs. Squares:
A square is a special type of rectangle where all four sides are equal in length. While a square also has two pairs of parallel sides (inheriting this property from the rectangle), its additional property of equal sides distinguishes it.
Rectangles vs. Parallelograms:
A parallelogram is a quadrilateral with two pairs of parallel sides. However, unlike a rectangle, a parallelogram's angles are not necessarily right angles. A rectangle is a special case of a parallelogram where all angles are right angles.
Rectangles vs. Rhombuses:
A rhombus is a quadrilateral with all four sides equal in length. While it has two pairs of parallel sides (similar to a square), its angles are not necessarily right angles, unlike a rectangle.
Real-World Applications of Rectangles and Parallelism
The properties of rectangles, especially the parallelism of their sides, are exploited extensively in various fields:
- Architecture and Construction: Buildings, rooms, windows, and doors are often rectangular due to their stability and ease of construction. The parallel sides allow for precise measurements and efficient construction techniques.
- Graphic Design and Art: Rectangles are fundamental shapes in graphic design and art, providing a structured framework for layouts and compositions. The parallel sides aid in creating balanced and visually appealing designs.
- Manufacturing and Engineering: Many manufactured products, from electronic devices to furniture, incorporate rectangular shapes because of their ease of production and efficient use of materials. The parallel sides simplify manufacturing processes and ensure consistency.
- Everyday Objects: Numerous everyday objects, from books and photographs to screens and tables, utilize rectangular shapes because of their practicality and functionality.
Mathematical Proofs and the Parallel Postulate
The parallelism of a rectangle's sides is not just an observed property; it's a consequence of fundamental axioms and postulates in Euclidean geometry. The parallel postulate, a key assumption in Euclidean geometry, states that through a point not on a given line, there is exactly one line parallel to the given line. This postulate is crucial in proving many properties of rectangles, including the parallelism of its sides. Formal geometric proofs would rely on this postulate and other geometric theorems to rigorously demonstrate the existence of these parallel pairs.
Beyond the Basics: Advanced Concepts Related to Rectangles
Exploring the properties of rectangles opens doors to more advanced geometric concepts:
- Coordinate Geometry: Rectangles can be readily represented and analyzed using coordinate systems. Their vertices can be defined by coordinates, and properties like area and perimeter can be calculated using algebraic methods.
- Vector Geometry: Vectors can be used to represent the sides of a rectangle, enabling the use of vector algebra to analyze its properties and relationships with other geometric objects.
- Transformations: Rectangles can be transformed—rotated, reflected, or translated—using geometric transformations. These transformations preserve the essential properties of the rectangle, such as the parallelism of its sides.
- Higher Dimensional Analogues: The concept of a rectangle extends to higher dimensions. In three dimensions, a rectangular prism (cuboid) possesses three pairs of parallel faces. This concept can be further generalized to higher dimensions.
Conclusion: The Undeniable Parallelism of Rectangles
To reiterate, a rectangle unequivocally possesses two pairs of parallel sides. This fundamental property is not just a characteristic; it's the cornerstone of its many useful properties and wide-ranging applications. Understanding this seemingly simple fact allows for a deeper appreciation of the elegance and practicality of this ubiquitous geometric shape, underscoring its importance in mathematics, science, and everyday life. The exploration of rectangles extends far beyond the simple answer to our initial question, revealing a rich tapestry of geometric concepts and their real-world significance. From basic definitions to advanced mathematical applications, the rectangle's parallel sides remain a central element in its multifaceted nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Pairs Of Parallel Sides Does A Rectangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.