How Many Sides Has A Octagon
News Co
Apr 06, 2025 · 5 min read
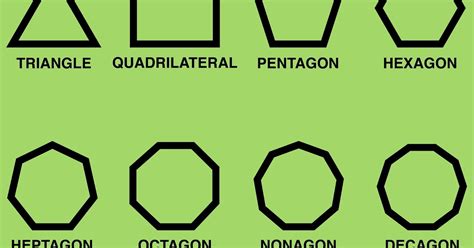
Table of Contents
How Many Sides Does an Octagon Have? A Deep Dive into Octagonal Geometry
The question, "How many sides does an octagon have?" seems simple enough. The answer, of course, is eight. But let's delve deeper than a simple one-word response. This article will explore the fascinating world of octagons, examining their properties, applications, and the mathematical concepts that define them. We'll move beyond the basic definition and uncover the rich geometry hidden within this eight-sided polygon.
Understanding Polygons: A Foundation for Octagons
Before we fully immerse ourselves in the octagon, let's establish a firm understanding of polygons in general. A polygon is a closed two-dimensional figure formed by connecting a set of straight line segments. These segments are called the sides of the polygon, and the points where the segments meet are called vertices or angles.
Polygons are classified based on the number of sides they have:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon (or Septagon): 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
- And so on...
The number of sides directly dictates many of the polygon's properties, including its internal angles and the possibilities for its symmetry.
The Octagon: An Eight-Sided Shape
Now, let's focus our attention on the octagon – the subject of our inquiry. An octagon, by definition, is a polygon with eight sides. These eight sides enclose a region in a plane, creating a shape with various interesting geometrical properties.
Types of Octagons
Not all octagons are created equal. They can be categorized into different types based on their properties:
-
Regular Octagon: A regular octagon has all eight sides of equal length and all eight interior angles of equal measure. Each interior angle of a regular octagon measures 135 degrees (calculated using the formula (n-2) * 180 / n, where 'n' is the number of sides). This symmetry makes regular octagons aesthetically pleasing and frequently used in design.
-
Irregular Octagon: An irregular octagon has sides of varying lengths and angles of varying measures. There's a vast range of possibilities for irregular octagons, making them highly versatile shapes.
Calculating the Interior Angles of an Octagon
As mentioned earlier, the interior angles of a regular octagon are all equal to 135 degrees. This can be calculated using the formula for the sum of interior angles of a polygon: (n - 2) * 180°, where 'n' is the number of sides. For an octagon (n=8), the sum of the interior angles is (8 - 2) * 180° = 1080°. Since it's a regular octagon, we divide this sum by 8 to find the measure of each individual angle: 1080° / 8 = 135°.
For irregular octagons, the sum of the interior angles remains 1080°, but the individual angles will vary.
Applications of Octagons in Real Life
Octagons are surprisingly common in various aspects of our lives, often appearing in architecture, design, and even nature:
Architecture and Design
-
Stop Signs: One of the most recognizable applications of an octagon is the classic stop sign. The distinctive shape is easily identifiable from a distance, improving road safety.
-
Buildings and Structures: Octagonal shapes can be found in the designs of some buildings and structures, offering unique architectural features and visual appeal. Octagonal towers and rooms provide interesting spatial dynamics.
-
Tiles and Mosaics: Octagonal tiles are frequently used in flooring, wall coverings, and mosaics, creating intricate and visually striking patterns.
-
Tabletops and Furniture: Octagonal tabletops and other pieces of furniture add a touch of unique style to interior design.
Nature
While less prevalent than squares or hexagons, octagonal shapes can sometimes be observed in nature, although often imperfectly formed. Certain crystals and naturally occurring formations might exhibit approximate octagonal symmetry.
Other Applications
Beyond architecture and nature, octagons are used in:
-
Games and Puzzles: Octagonal shapes appear in various games and puzzles, adding an element of unique gameplay.
-
Logos and Branding: The octagon’s unique shape can be incorporated into logos and branding designs to create a memorable visual identity.
Exploring the Mathematics of Octagons
Beyond their visual appeal and practical applications, octagons offer rich mathematical opportunities for exploration:
Area Calculation
The area of a regular octagon can be calculated using the following formula:
Area = 2(1 + √2) * s²
where 's' is the length of one side.
For irregular octagons, the area calculation becomes more complex and might require breaking the octagon into smaller, simpler shapes (like triangles or quadrilaterals) and summing their areas.
Tessellations
Octagons can be used to create tessellations, which are patterns formed by repeating a shape without gaps or overlaps. However, regular octagons alone cannot tessellate a plane. They need to be combined with other shapes, often squares, to achieve a complete covering.
Symmetry
Regular octagons possess a high degree of symmetry. They have eight lines of reflectional symmetry and eight rotational symmetries. This symmetrical nature contributes to their aesthetic appeal and their use in decorative patterns.
Beyond the Basics: Advanced Octagonal Geometry
For those interested in a deeper exploration, there are advanced concepts related to octagons:
-
Inscribed and Circumscribed Circles: A circle can be inscribed within a regular octagon (tangent to each side) and a circle can be circumscribed around a regular octagon (passing through each vertex). The radii of these circles are related to the side length of the octagon.
-
Star Octagons: By extending the sides of a regular octagon, you can create a star octagon, also known as an octagram. These star polygons have their own interesting geometrical properties.
-
Three-Dimensional Octagonal Structures: Octagons can form the basis of three-dimensional shapes and structures. Consider octagonal prisms or pyramids as examples.
Conclusion: The Enduring Fascination of the Octagon
While the simple answer to "How many sides does an octagon have?" is eight, the journey into the world of octagonal geometry reveals a fascinating depth. From its applications in everyday life to its rich mathematical properties, the octagon is a shape worthy of further exploration. Its unique combination of symmetry and versatility continues to inspire architects, designers, mathematicians, and artists alike. Hopefully, this comprehensive exploration has provided you with a much deeper understanding of this eight-sided shape and its significance. Remember that even the simplest geometric figures hold a wealth of complex and intriguing information.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Sides Has A Octagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.