How Many Sixths Are Equivalent To 2/3
News Co
Apr 26, 2025 · 5 min read
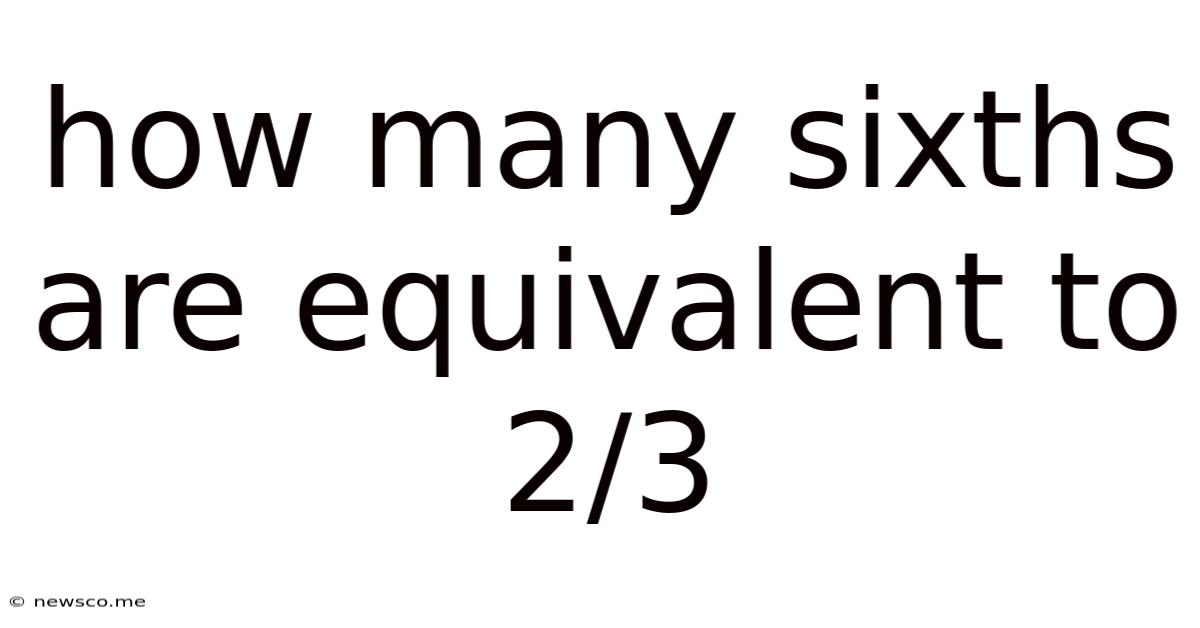
Table of Contents
How Many Sixths Are Equivalent to 2/3? A Deep Dive into Fraction Equivalence
Understanding fraction equivalence is a cornerstone of mathematical literacy. This seemingly simple question – "How many sixths are equivalent to 2/3?" – opens the door to a broader exploration of fractions, their representations, and the crucial concept of finding common denominators. This article will not only answer the question directly but will also delve into the underlying principles, providing you with a comprehensive understanding of fraction equivalence and offering practical methods for solving similar problems.
Understanding Fractions: A Quick Refresher
Before we tackle the main question, let's briefly review the fundamental components of a fraction:
- Numerator: The top number in a fraction, representing the number of parts you have.
- Denominator: The bottom number in a fraction, representing the total number of equal parts in a whole.
A fraction, such as 2/3, signifies that you have 2 parts out of a total of 3 equal parts. Understanding this basic structure is crucial for grasping fraction equivalence.
The Concept of Fraction Equivalence
Two fractions are equivalent if they represent the same proportion or amount, even if they look different. This means they occupy the same position on a number line. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. All these fractions represent exactly half of a whole.
The key to understanding fraction equivalence lies in the relationship between the numerator and the denominator. Equivalent fractions are created by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process doesn't change the fundamental value of the fraction; it simply changes its representation.
Finding Equivalent Fractions: A Step-by-Step Approach
To find out how many sixths are equivalent to 2/3, we need to find a fraction with a denominator of 6 that represents the same value as 2/3. We can achieve this using the following steps:
1. Identify the Target Denominator: Our goal is to find an equivalent fraction with a denominator of 6.
2. Determine the Multiplication Factor: Compare the original denominator (3) to the target denominator (6). To transform 3 into 6, we need to multiply by 2 (3 x 2 = 6).
3. Apply the Multiplication Factor: Crucially, to maintain equivalence, we must multiply both the numerator and the denominator of the original fraction by the same factor (2).
Therefore: (2/3) x (2/2) = 4/6
This calculation demonstrates that 4/6 is equivalent to 2/3. Therefore, there are four sixths in 2/3.
Visualizing Fraction Equivalence
Visual aids can significantly enhance understanding. Imagine a circle divided into three equal parts. Shading two of these parts represents 2/3. Now, imagine the same circle divided into six equal parts. Shading four of these six parts would represent 4/6. You'll visually confirm that both representations cover the same area, proving their equivalence. This visual approach is particularly helpful for those who benefit from concrete representations.
Different Methods for Finding Equivalent Fractions
While the method described above is straightforward, several other methods can be used to find equivalent fractions. Let's explore some of them:
1. Using Cross-Multiplication: This method is useful for determining if two fractions are equivalent. Cross-multiply the numerator of one fraction by the denominator of the other, and vice-versa. If the products are equal, the fractions are equivalent. For example:
2/3 and 4/6: (2 x 6) = 12 and (3 x 4) = 12. Since the products are equal, the fractions are equivalent.
2. Simplifying Fractions: This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. Simplifying a fraction reduces it to its simplest form, often revealing its equivalence to other fractions. For instance, simplifying 4/6 by dividing both by their GCD (2) gives 2/3.
3. Using a Fraction Calculator: While not as insightful as manual methods, fraction calculators can quickly determine if two fractions are equivalent or find an equivalent fraction with a specific denominator. These tools can be helpful for verifying your calculations.
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is essential in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. Fraction equivalence is crucial for accurately converting measurements.
-
Construction and Engineering: Precise measurements are paramount in these fields. Fraction equivalence ensures accurate calculations and material estimations.
-
Finance and Accounting: Managing budgets and calculating proportions necessitates a solid grasp of fractions and their equivalence.
-
Data Analysis: Representing and comparing proportions in data often involves working with fractions and their equivalent forms.
Beyond the Basics: Exploring More Complex Fraction Problems
The principle of equivalence extends beyond simple fraction manipulations. Consider problems involving adding, subtracting, multiplying, or dividing fractions. Finding common denominators—a crucial step in these operations—relies heavily on understanding fraction equivalence. Without the ability to identify and create equivalent fractions, performing complex fraction calculations becomes significantly more challenging.
Conclusion: Mastering Fraction Equivalence for Mathematical Fluency
The ability to determine how many sixths are equivalent to 2/3, and more generally to work confidently with fraction equivalence, is fundamental to mathematical proficiency. This skill empowers you to solve a wide array of problems, from everyday calculations to more complex mathematical tasks. By understanding the underlying principles and employing the various methods discussed in this article, you can strengthen your grasp of fractions and build a strong foundation for future mathematical endeavors. Remember, practice is key to mastering any mathematical concept, so continue to work with fractions to enhance your understanding and proficiency. The ability to easily manipulate and interpret fractions will serve you well throughout your educational journey and in numerous real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Sixths Are Equivalent To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.