How Many Symmetry Lines Does A Octagon Have
News Co
Apr 08, 2025 · 5 min read
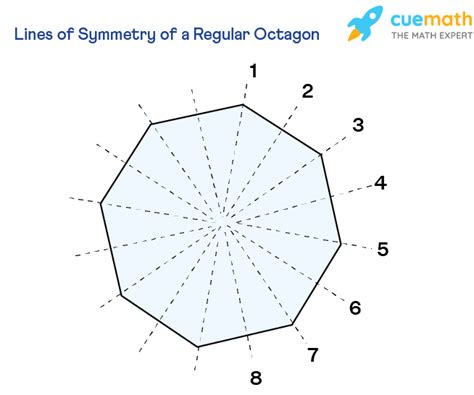
Table of Contents
How Many Lines of Symmetry Does an Octagon Have? A Comprehensive Exploration
Symmetry, a fundamental concept in mathematics and geometry, describes the harmonious balance and proportional arrangement of elements within a shape or object. Understanding lines of symmetry is crucial in various fields, from art and design to engineering and crystallography. This article delves deep into the fascinating world of symmetry, focusing specifically on the number of lines of symmetry possessed by a regular octagon. We will explore the definition of symmetry, different types of symmetry, and then meticulously determine the lines of symmetry present in an octagon.
What is Symmetry?
Symmetry, at its core, implies a sense of balance and proportionality. In geometry, it refers to the property of a shape remaining unchanged after undergoing certain transformations, such as reflection, rotation, or translation. These transformations leave the shape looking exactly the same as it did before the transformation. This unchanging characteristic is the essence of symmetry.
Types of Symmetry
There are several types of symmetry, each characterized by its own unique transformation:
-
Reflectional Symmetry (Line Symmetry): This is the most common type of symmetry we encounter. A shape possesses reflectional symmetry if it can be folded along a line (called the line of symmetry or axis of symmetry) such that the two halves perfectly overlap. This line divides the shape into two mirror images.
-
Rotational Symmetry: A shape exhibits rotational symmetry if it can be rotated about a central point by a certain angle (less than 360 degrees) and still look identical to its original position. The angle of rotation is a fraction of 360 degrees, and the number of times the shape looks identical during a full 360-degree rotation determines its order of rotational symmetry.
-
Translational Symmetry: This type of symmetry occurs in patterns that repeat themselves in a specific direction. Translating the pattern along a certain vector leaves the pattern unchanged.
Exploring the Octagon
An octagon is a polygon with eight sides and eight angles. A regular octagon is a special type of octagon where all sides are equal in length, and all angles are equal in measure (135 degrees). It's the regular octagons that we will be primarily focusing on in our investigation of lines of symmetry.
Identifying Lines of Symmetry in a Regular Octagon
To determine the number of lines of symmetry in a regular octagon, we need to systematically consider all possible lines that could potentially act as axes of reflection.
Lines of Symmetry Through Opposite Vertices
First, let's examine lines that pass through opposite vertices of the octagon. A regular octagon has four pairs of opposite vertices. Each line connecting a pair of opposite vertices acts as a line of symmetry because reflecting the octagon across this line results in a perfect overlap. Therefore, we have four lines of symmetry of this type.
Lines of Symmetry Through Midpoints of Opposite Sides
Next, let's consider lines that pass through the midpoints of opposite sides. A regular octagon has four pairs of opposite sides. Drawing a line connecting the midpoints of each pair of opposite sides again creates a line of symmetry. Reflecting the octagon across any of these lines will result in the same image. This gives us another four lines of symmetry.
Total Lines of Symmetry in a Regular Octagon
By combining the lines of symmetry passing through opposite vertices and the lines of symmetry passing through midpoints of opposite sides, we arrive at the total number of lines of symmetry in a regular octagon: 4 + 4 = 8.
Therefore, a regular octagon possesses a total of eight lines of symmetry.
Lines of Symmetry in Irregular Octagons
It's important to note that the number of lines of symmetry changes significantly if the octagon is irregular (meaning its sides and angles are not all equal). An irregular octagon may possess fewer lines of symmetry, or even none at all, depending on the specific arrangement of its sides and angles. The eight lines of symmetry are a unique characteristic of the regular octagon.
Symmetry and Rotational Symmetry in a Regular Octagon
While we've primarily focused on reflectional symmetry (lines of symmetry), it's worth mentioning the rotational symmetry of a regular octagon. A regular octagon has rotational symmetry of order 8. This means it can be rotated about its center by angles of 45 degrees (360/8), 90 degrees, 135 degrees, and so on, and still look identical. This rotational symmetry is closely related to its reflectional symmetry.
Applications of Symmetry in Real Life
Understanding symmetry is crucial in many real-world applications. Here are a few examples:
-
Architecture and Design: Symmetrical designs are aesthetically pleasing and often used in buildings, bridges, and other structures. The balance and harmony created by symmetry enhance the visual appeal and structural integrity.
-
Art and Nature: Symmetry is a prominent feature in art, particularly in geometric patterns, Islamic art, and many natural formations like snowflakes and flowers.
-
Engineering: Engineers use symmetry principles to design efficient and balanced structures, such as aircraft and automobiles. Symmetrical designs often provide better stability and performance.
-
Crystallography: Symmetry plays a vital role in understanding the structure of crystals. The arrangement of atoms in a crystal lattice often exhibits various types of symmetry, which helps scientists classify and understand the properties of different crystals.
Conclusion: The Eightfold Symmetry of the Regular Octagon
In conclusion, a regular octagon possesses eight lines of symmetry – four passing through opposite vertices and four passing through midpoints of opposite sides. This characteristic makes the regular octagon a geometric figure with a high degree of symmetry, impacting its visual appeal and mathematical properties. Understanding this symmetry is not just an abstract mathematical concept; it has practical implications in various fields, demonstrating the pervasive nature of symmetry in our world. This exploration highlights the beauty and importance of geometrical symmetry, particularly in the specific case of the regular octagon and its eight lines of reflectional symmetry. Further exploration into other polygons and their symmetries would offer similar insights into the principles governing geometric harmony and balance.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Symmetry Lines Does A Octagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.