How Many Terms Are In The Expression Shown 2n+5-3p+4q
News Co
May 09, 2025 · 4 min read
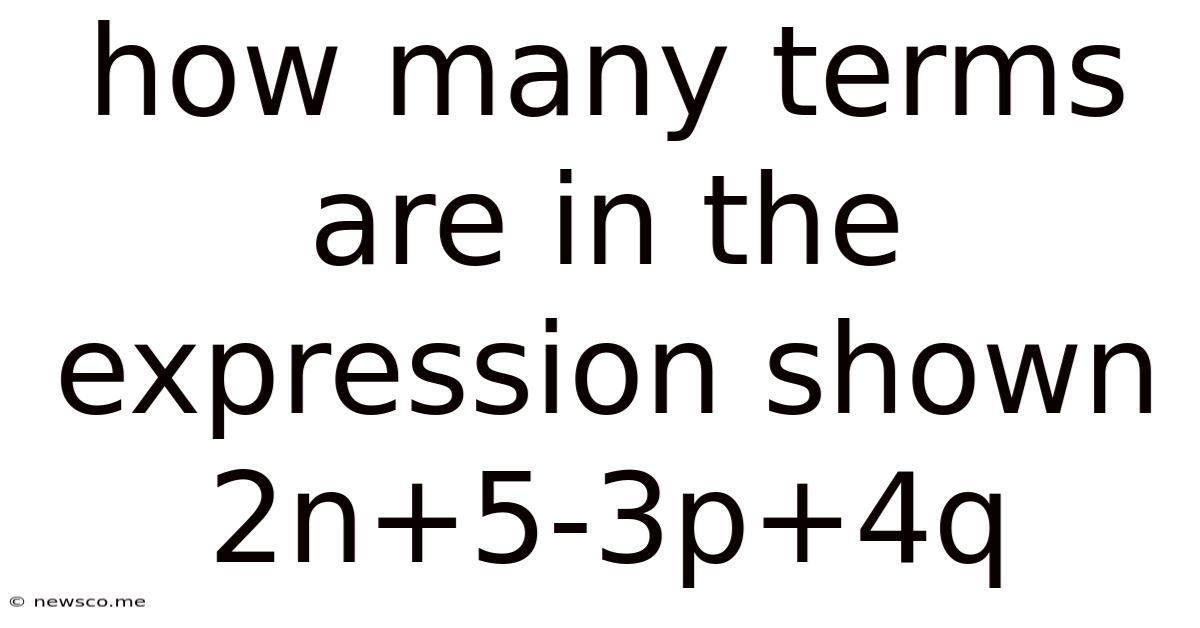
Table of Contents
How Many Terms Are in the Expression 2n + 5 - 3p + 4q? Understanding Algebraic Expressions
This seemingly simple question, "How many terms are in the expression 2n + 5 - 3p + 4q?", opens the door to a deeper understanding of algebraic expressions, a fundamental concept in mathematics. While the answer itself is straightforward, exploring the underlying principles allows us to build a stronger foundation for more complex algebraic manipulations. Let's delve into the details.
Defining Terms in Algebraic Expressions
Before we answer the question directly, let's clarify what constitutes a "term" in an algebraic expression. A term is a single number, a variable, or a number multiplied by a variable or variables. Terms are separated by addition or subtraction signs. Crucially, multiplication and division within a term do not separate it into multiple terms.
Consider the expression 2n + 5 - 3p + 4q. Let's break it down:
- 2n: This is a term. It consists of a coefficient (2) and a variable (n) multiplied together.
- 5: This is also a term. It's a constant term, meaning it's a number without any variables.
- -3p: This is a term. The negative sign is part of the term. It indicates a coefficient of -3 multiplied by the variable p.
- 4q: This is a term. It's a positive term, with a coefficient of 4 multiplied by the variable q.
Identifying the Terms: A Step-by-Step Guide
To clearly identify terms, follow these steps:
- Look for addition and subtraction signs: These are the separators between terms.
- Treat anything between consecutive addition or subtraction signs as a single term: Even if that term contains multiplication or division, it remains one unit.
- Include the sign before each term: The sign directly preceding a term indicates whether it's positive or negative.
Applying this to our expression, 2n + 5 - 3p + 4q:
- The first term is +2n (the '+' is often implied but is there).
- The second term is +5.
- The third term is -3p.
- The fourth term is +4q.
Therefore, there are four terms in the expression 2n + 5 - 3p + 4q.
Beyond the Basics: Exploring Different Types of Algebraic Expressions
Understanding terms is crucial for working with various types of algebraic expressions. Let's look at a few examples:
Monomials: Expressions with One Term
A monomial is an algebraic expression consisting of only one term. Examples include:
- 3x
- -7y²
- 5
Binomials: Expressions with Two Terms
A binomial is an algebraic expression containing two terms. Examples include:
- x + y
- 2a - 5b
- 4m² + 6n
Trinomials: Expressions with Three Terms
A trinomial is an algebraic expression with three terms. Examples include:
- x² + 2x + 1
- a² - b² + c²
- 3y³ - 7y + 2
Polynomials: Expressions with Multiple Terms
A polynomial is a general term that encompasses expressions with one or more terms. Monomials, binomials, and trinomials are all specific types of polynomials.
The Importance of Understanding Terms in Algebra
The ability to correctly identify terms is fundamental to numerous algebraic operations:
- Combining like terms: This involves adding or subtracting terms that have the same variables raised to the same powers. For instance, in the expression 3x + 2x - 5, we can combine the like terms 3x and 2x to get 5x, simplifying the expression to 5x - 5.
- Expanding expressions: This often involves removing parentheses using the distributive property. Understanding terms helps us to correctly apply the distributive property and combine like terms afterward.
- Factoring expressions: This involves rewriting an expression as a product of simpler expressions. Identifying terms is crucial for recognizing common factors.
- Solving equations: Manipulating equations to isolate variables relies heavily on understanding and correctly working with individual terms.
Advanced Applications: Dealing with more Complex Expressions
Let's consider more complex expressions to solidify our understanding:
Example 1: 3x²y + 5xy² - 2xyz + 7
This expression has four terms: 3x²y, 5xy², -2xyz, and 7. Note that even though some terms contain multiple variables, they are still single terms due to the multiplication of these variables.
Example 2: (2a + 3b)(c - d)
Before counting terms, we need to expand this expression using the distributive property (FOIL method):
(2a + 3b)(c - d) = 2ac - 2ad + 3bc - 3bd
Now, we can clearly see that the expanded expression has four terms: 2ac, -2ad, 3bc, and -3bd.
Example 3: 5/(2x + y)
This is not four terms. The entire expression 5/(2x+y) is one single term, as division is an operation within the term. It's a fraction where the numerator (5) and the denominator (2x + y) are considered a single entity.
Common Mistakes and How to Avoid Them
A frequent error is misinterpreting multiplication or division as term separators. Remember, addition and subtraction are the only operations that define the boundaries between terms.
Conclusion: Mastering Terms in Algebraic Expressions
The seemingly straightforward question of how many terms are in 2n + 5 - 3p + 4q provides a springboard to understanding the foundational elements of algebraic expressions. By accurately identifying terms, you'll master essential skills for simplifying, manipulating, and solving a wide range of algebraic problems. This knowledge forms the bedrock for more advanced algebraic concepts and is essential for success in mathematics and related fields. Continue practicing with various examples to further solidify your grasp of these principles. Remember to focus on identifying the addition and subtraction signs to accurately delineate each term.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about How Many Terms Are In The Expression Shown 2n+5-3p+4q . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.