How Many Vertices Does A Rectangular Pyramid Have
News Co
Apr 06, 2025 · 6 min read
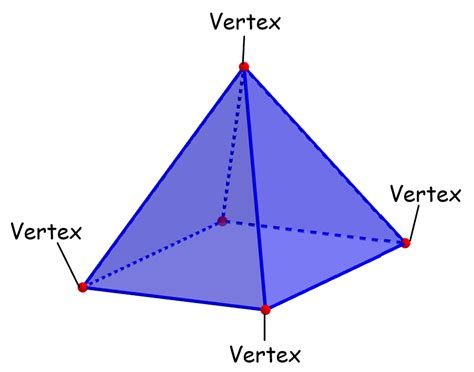
Table of Contents
How Many Vertices Does a Rectangular Pyramid Have? A Deep Dive into Geometry
Understanding the fundamental properties of three-dimensional shapes is crucial in various fields, from architecture and engineering to computer graphics and game development. One such shape, the rectangular pyramid, often sparks curiosity regarding its constituent parts, particularly the number of vertices it possesses. This article will delve into a comprehensive exploration of rectangular pyramids, clarifying the concept of vertices and explaining why a rectangular pyramid has exactly five vertices. We will also explore related concepts and provide practical applications to solidify your understanding.
What is a Rectangular Pyramid?
Before we determine the number of vertices, let's clearly define what a rectangular pyramid is. A rectangular pyramid is a three-dimensional geometric shape with a rectangular base and four triangular faces that meet at a single point called the apex. Imagine a square-based tent; that's a perfect real-world example of a rectangular pyramid.
The key characteristics that define a rectangular pyramid are:
-
Rectangular Base: The foundation of the pyramid is a rectangle. This base provides the structure upon which the triangular faces are built. The dimensions of the rectangle (length and width) contribute to the overall size and shape of the pyramid.
-
Triangular Faces: Four triangular faces rise from the edges of the rectangular base, converging at a single point. These faces are not necessarily equilateral or isosceles; their dimensions depend on the height of the pyramid and the dimensions of the rectangular base.
-
Apex: The single point where all four triangular faces meet is known as the apex. This point is located directly above (or below, depending on orientation) the center of the rectangular base. The distance from the apex to the base significantly influences the pyramid's overall height and shape.
-
Edges: A rectangular pyramid has eight edges: four forming the base rectangle and four connecting the base vertices to the apex. These edges are line segments that define the boundaries between the faces.
Understanding Vertices in Geometry
A vertex (plural: vertices) in geometry is a point where two or more lines or edges meet. It's a crucial element in defining the shape and structure of any polyhedron (a three-dimensional shape with flat faces). Think of vertices as the "corners" of a shape.
In simpler terms, a vertex represents a corner or a point where lines intersect. For instance, a square has four vertices, a cube has eight, and a triangular prism has six. Understanding this concept is fundamental to comprehending the geometry of various 3D shapes.
Counting the Vertices of a Rectangular Pyramid
Now, let's apply our understanding of vertices to the rectangular pyramid. To count the vertices accurately, we examine the points where edges meet:
-
Base Vertices: The rectangular base itself has four vertices – one at each corner of the rectangle.
-
Apex Vertex: The apex, the single point where all four triangular faces meet, constitutes the fifth vertex.
Therefore, a rectangular pyramid has a total of five vertices. This is a constant; regardless of the size or proportions of the rectangular base or the height of the pyramid, the number of vertices remains five.
Exploring Related Geometric Concepts
Understanding the number of vertices of a rectangular pyramid connects to broader geometric concepts:
-
Euler's Formula: This fundamental theorem in geometry relates the number of vertices (V), edges (E), and faces (F) of any convex polyhedron (a polyhedron where all faces are flat and no indentations). The formula states: V - E + F = 2. For a rectangular pyramid (V = 5, E = 8, F = 5), this formula holds true: 5 - 8 + 5 = 2.
-
Polyhedra Classification: Rectangular pyramids are classified as polyhedra, specifically as right pyramids (if the apex is directly above the center of the base) or oblique pyramids (if the apex is not directly above the center). Understanding these classifications helps categorize and analyze different types of three-dimensional shapes.
-
Surface Area and Volume Calculations: The number of vertices, although not directly involved in the calculations, contributes to understanding the overall structure of the pyramid, influencing the formulas used to compute its surface area and volume. These calculations are vital in engineering and architectural applications.
Practical Applications of Rectangular Pyramid Knowledge
The understanding of rectangular pyramids and their properties finds its way into diverse fields:
-
Architecture: Architects use rectangular pyramids in designing structures, ranging from simple roof designs to more complex monumental constructions. Accurate calculation of dimensions, based on the understanding of vertices, edges, and faces, is crucial for structural integrity.
-
Engineering: In civil engineering, understanding the geometry of rectangular pyramids is essential for designing supporting structures, calculating loads, and ensuring stability.
-
Computer Graphics and Game Development: Creating realistic 3D models in computer graphics and video games requires a thorough grasp of geometric shapes like rectangular pyramids. The precise definition of vertices, faces, and edges is essential for creating accurate and visually appealing models.
-
Packaging and Design: The shape of a rectangular pyramid can be optimized for packaging and efficient storage of goods, reducing wasted space and improving logistics.
-
Mathematics Education: Learning about rectangular pyramids is crucial for developing spatial reasoning and problem-solving skills in mathematics education. Understanding their properties provides a strong foundation for further studies in geometry and related fields.
Beyond the Basics: Variations and Extensions
While we've focused on the standard rectangular pyramid, several variations exist:
-
Oblique Rectangular Pyramids: In an oblique rectangular pyramid, the apex is not directly above the center of the rectangular base. This shifts the geometry slightly, changing the lengths of the edges and potentially the angles of the triangular faces, but the number of vertices remains at five.
-
Truncated Rectangular Pyramids: A truncated rectangular pyramid is one where the apex has been cut off by a plane parallel to the base, resulting in a second rectangular base. This adds four more vertices, bringing the total to nine.
-
Regular Rectangular Pyramids: If the base is a square and the apex is directly above the center of the base, it's termed a regular rectangular pyramid. This symmetry simplifies many calculations but doesn't affect the vertex count.
Conclusion: The Five Vertices of a Rectangular Pyramid
In conclusion, a rectangular pyramid, irrespective of its size or proportions, always possesses five vertices. This seemingly simple fact underscores a fundamental principle in geometry: understanding the fundamental properties of shapes is crucial for numerous applications across diverse fields. From the practical applications in engineering and architecture to the theoretical foundations in mathematics, grasping the concept of vertices and their role in defining three-dimensional shapes remains an essential aspect of geometric literacy. This article has provided a detailed explanation, solidifying the understanding of rectangular pyramids and their properties while exploring related geometric concepts and real-world applications. By understanding these foundational aspects, you can tackle more complex geometric problems and contribute to a more profound understanding of the three-dimensional world.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many Vertices Does A Rectangular Pyramid Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.