How Much Bigger Is 7/8 Than 3/4
News Co
Apr 22, 2025 · 4 min read
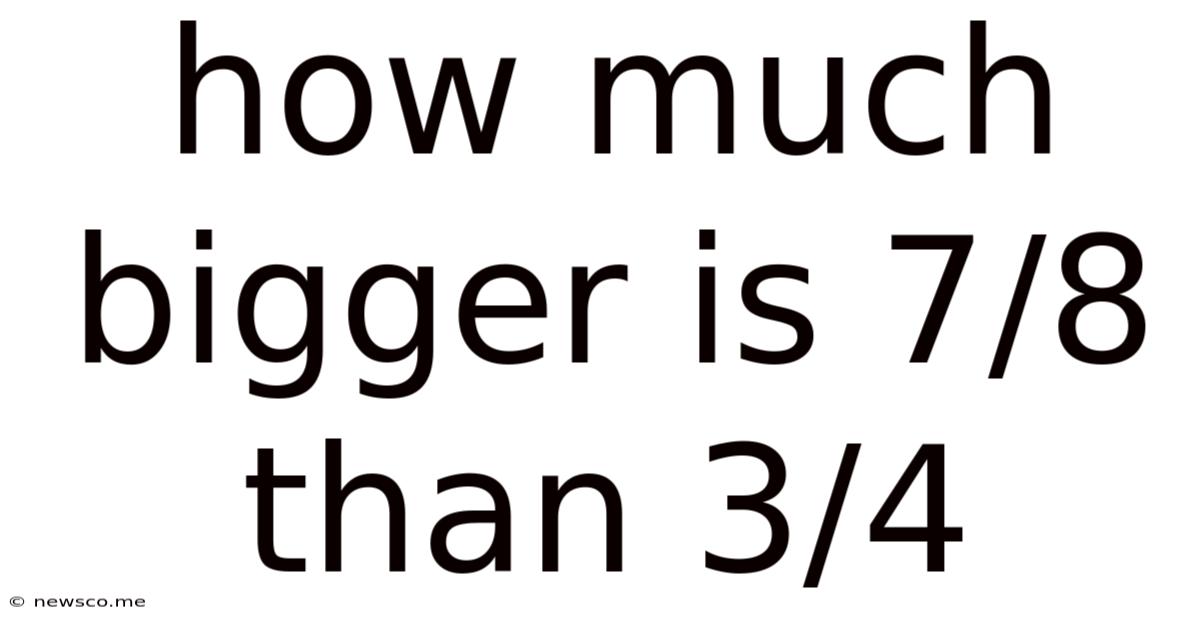
Table of Contents
How Much Bigger is 7/8 Than 3/4? A Deep Dive into Fraction Comparison
Comparing fractions might seem like a simple arithmetic task, but understanding the nuances of fraction comparison is crucial for a strong foundation in mathematics. This article delves deep into comparing 7/8 and 3/4, exploring various methods and expanding the understanding of fraction manipulation. We'll not only determine how much bigger 7/8 is than 3/4 but also equip you with the tools to tackle similar comparisons confidently.
Understanding Fractions: A Quick Refresher
Before we jump into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
The most straightforward method to compare fractions is to find a common denominator. This involves converting both fractions to equivalent fractions with the same denominator. Let's apply this to 7/8 and 3/4:
Finding the Least Common Multiple (LCM)
The least common multiple (LCM) of the denominators (8 and 4) is 8. Since 8 is already the denominator of 7/8, we only need to convert 3/4 to an equivalent fraction with a denominator of 8.
To do this, we multiply both the numerator and the denominator of 3/4 by 2:
(3 × 2) / (4 × 2) = 6/8
Now we have both fractions with the same denominator: 7/8 and 6/8.
Comparing the Numerators
Comparing the numerators, we see that 7 is greater than 6. Therefore, 7/8 is greater than 6/8 (which is equivalent to 3/4).
Determining the Difference
To find out how much bigger 7/8 is than 3/4, we subtract the smaller fraction from the larger fraction:
7/8 - 6/8 = 1/8
Therefore, 7/8 is 1/8 bigger than 3/4.
Method 2: Converting to Decimals
Another effective method for comparing fractions involves converting them into decimals. This method is particularly useful when dealing with more complex fractions or when a numerical difference is required.
Converting Fractions to Decimals
To convert a fraction to a decimal, simply divide the numerator by the denominator:
7/8 = 0.875
3/4 = 0.75
Comparing Decimals
Comparing the decimal values, we find that 0.875 is greater than 0.75.
Calculating the Difference
Subtracting the smaller decimal from the larger decimal gives us the difference:
0.875 - 0.75 = 0.125
Since 0.125 is equivalent to 1/8, this confirms our previous finding: 7/8 is 1/8 bigger than 3/4.
Method 3: Visual Representation
Visualizing fractions can significantly aid in understanding their relative sizes. Consider representing each fraction using a circle or rectangle divided into equal parts.
Visualizing 3/4
Draw a circle and divide it into four equal parts. Shade three of those parts to represent 3/4.
Visualizing 7/8
Draw another circle of the same size and divide it into eight equal parts. Shade seven of those parts to represent 7/8.
Comparing the Visual Representations
By comparing the shaded areas, it becomes visually apparent that 7/8 represents a larger portion of the whole compared to 3/4. While this method doesn't directly calculate the difference, it provides a strong intuitive understanding of the comparison.
Expanding the Understanding: Working with Different Denominators
The methods described above are universally applicable to comparing any two fractions. The key is to find a common denominator or convert the fractions to decimals. Let's explore an example with different denominators:
Compare 5/6 and 2/3
Method 1: Common Denominator
The LCM of 6 and 3 is 6. We only need to convert 2/3:
2/3 = (2 × 2) / (3 × 2) = 4/6
Now compare 5/6 and 4/6. 5/6 is greater than 4/6 by 1/6.
Method 2: Decimal Conversion
5/6 ≈ 0.833
2/3 ≈ 0.667
0.833 - 0.667 ≈ 0.167 (approximately 1/6)
Practical Applications: Real-World Examples
Understanding fraction comparison is vital in numerous real-world scenarios:
- Cooking and Baking: Following recipes often requires understanding fractions for accurate measurements.
- Construction and Engineering: Precise measurements and calculations are essential, relying heavily on fraction manipulation.
- Finance: Calculating proportions, percentages, and interest rates involves working with fractions.
- Data Analysis: Representing data using fractions and percentages is common in various fields.
Conclusion: Mastering Fraction Comparison
Comparing fractions, such as determining how much bigger 7/8 is than 3/4, is a fundamental skill with widespread applications. By mastering the techniques of finding common denominators or converting to decimals, you can confidently compare any two fractions and calculate their precise difference. Remember, understanding the underlying concepts and choosing the most efficient method for a particular problem is key to success in mathematics and beyond. Visual representations can aid understanding, especially for beginners, reinforcing the numerical comparisons. This in-depth exploration should provide a comprehensive understanding of fraction comparison and empower you to confidently tackle similar problems in various contexts. The ability to efficiently compare and manipulate fractions is a cornerstone of mathematical literacy and practical problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Much Bigger Is 7/8 Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.