How Much Is 1/3 And 1/3
News Co
Mar 31, 2025 · 6 min read
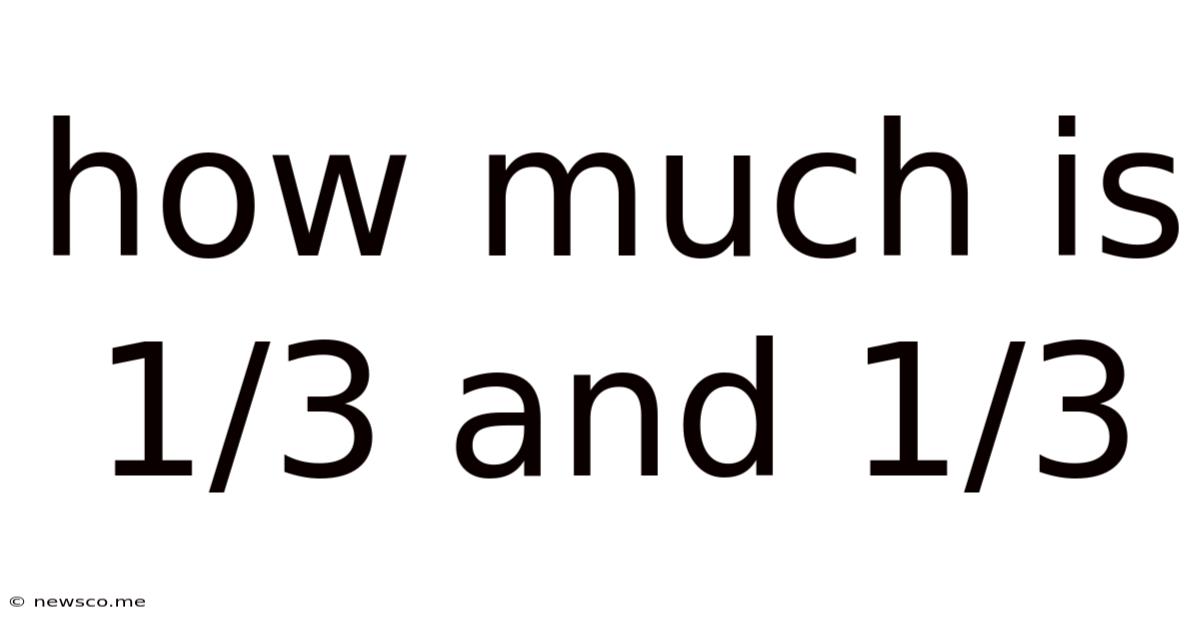
Table of Contents
How Much is 1/3 + 1/3? A Deep Dive into Fractions and Their Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This seemingly simple question, "How much is 1/3 + 1/3?", opens the door to exploring the world of fractions, their addition, and their practical uses. Let's delve into this topic comprehensively, covering the basics, advanced concepts, and real-world examples.
Understanding Fractions: A Refresher
Before tackling the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For instance, in the fraction 1/3, the denominator (3) signifies that the whole is divided into three equal parts, and the numerator (1) represents one of those parts.
Key Terminology:
- Numerator: The top number in a fraction. It indicates the number of parts being considered.
- Denominator: The bottom number in a fraction. It indicates the total number of equal parts the whole is divided into.
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 1/3, 2/5).
- Improper Fraction: A fraction where the numerator is equal to or greater than the denominator (e.g., 5/3, 7/4).
- Mixed Number: A combination of a whole number and a proper fraction (e.g., 1 2/3).
Adding Fractions: The Basics
Adding fractions with the same denominator is straightforward. You simply add the numerators together and keep the denominator the same.
Therefore, 1/3 + 1/3 = (1 + 1) / 3 = 2/3
This means that if you have one-third of something and add another one-third, you end up with two-thirds of that something.
Visual Representation:
Imagine a pizza cut into three equal slices. 1/3 represents one slice. Adding another 1/3 means you now have two slices, which is 2/3 of the pizza.
Real-World Examples:
- Baking: If a recipe calls for 1/3 cup of sugar and another 1/3 cup of flour, you would need a total of 2/3 cup of ingredients.
- Gardening: If you plant 1/3 of your garden with tomatoes and another 1/3 with peppers, you've used 2/3 of your garden space.
- Time Management: If you allocate 1/3 of your workday to meetings and another 1/3 to emails, you've spent 2/3 of your day on these activities.
Adding Fractions with Different Denominators
Adding fractions with different denominators requires finding a common denominator. This is a number that is a multiple of both denominators. Once you have a common denominator, you can convert both fractions to equivalent fractions with that denominator and then add them.
For example, let's add 1/3 and 1/2:
- Find a common denominator: The least common multiple of 3 and 2 is 6.
- Convert the fractions:
- 1/3 = 2/6 (multiply numerator and denominator by 2)
- 1/2 = 3/6 (multiply numerator and denominator by 3)
- Add the fractions: 2/6 + 3/6 = 5/6
Therefore, 1/3 + 1/2 = 5/6
Simplifying Fractions
Once you've added fractions, it's often necessary to simplify the result to its lowest terms. This means reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, the fraction 6/9 can be simplified:
The GCD of 6 and 9 is 3. Dividing both the numerator and denominator by 3 gives us 2/3.
Converting Improper Fractions to Mixed Numbers
When adding fractions results in an improper fraction (where the numerator is greater than or equal to the denominator), it's often helpful to convert it to a mixed number. A mixed number is a whole number and a proper fraction.
For example, let's convert the improper fraction 7/3 to a mixed number:
- Divide the numerator by the denominator: 7 ÷ 3 = 2 with a remainder of 1.
- The whole number part is the quotient: 2
- The fraction part is the remainder over the denominator: 1/3
Therefore, 7/3 = 2 1/3
Advanced Applications of Fractions
Fractions are used extensively in various fields:
- Engineering: Fractions are crucial in precise measurements and calculations in blueprints and structural design.
- Finance: Interest rates, stock prices, and financial ratios are often expressed as fractions or percentages (which are essentially fractions).
- Computer Science: Representing data and performing calculations in computer systems often involves fractions and their binary equivalents.
- Physics: Many physical quantities, such as velocities, accelerations, and forces, are calculated using fractions.
- Cooking and Baking: Recipes frequently use fractional measurements for ingredients.
Solving Word Problems Involving Fractions
Many real-world problems involve adding or subtracting fractions. Here's a step-by-step approach to solving such problems:
- Read the problem carefully: Identify the key information and what is being asked.
- Represent the information as fractions: Convert any given quantities into fractions.
- Perform the necessary operations: Add, subtract, multiply, or divide the fractions as required.
- Simplify the result: Reduce the answer to its simplest form.
- Check your answer: Make sure the answer makes sense in the context of the problem.
Example Word Problem:
John painted 1/3 of a fence on Monday and 1/3 of the fence on Tuesday. What fraction of the fence did he paint in total?
- Key information: John painted 1/3 on Monday and 1/3 on Tuesday.
- Representation: The amounts are already represented as fractions.
- Operation: Add the fractions: 1/3 + 1/3 = 2/3
- Simplification: The fraction 2/3 is already in its simplest form.
- Answer: John painted 2/3 of the fence in total.
Conclusion: The Importance of Understanding Fractions
Understanding fractions is a cornerstone of mathematical literacy and has far-reaching implications in various aspects of life. From everyday tasks like cooking and baking to complex calculations in engineering and finance, the ability to work comfortably with fractions is essential. This article has provided a comprehensive overview of fractions, their addition, and their practical applications, equipping you with the knowledge to confidently tackle fraction-related problems. Mastering fractions opens doors to further mathematical exploration and a deeper understanding of the quantitative world around us. Remember, practice makes perfect, so continue to work with fractions to solidify your understanding and improve your skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Much Is 1/3 And 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.