How Much Is 1 3 Of 100
News Co
Mar 17, 2025 · 5 min read
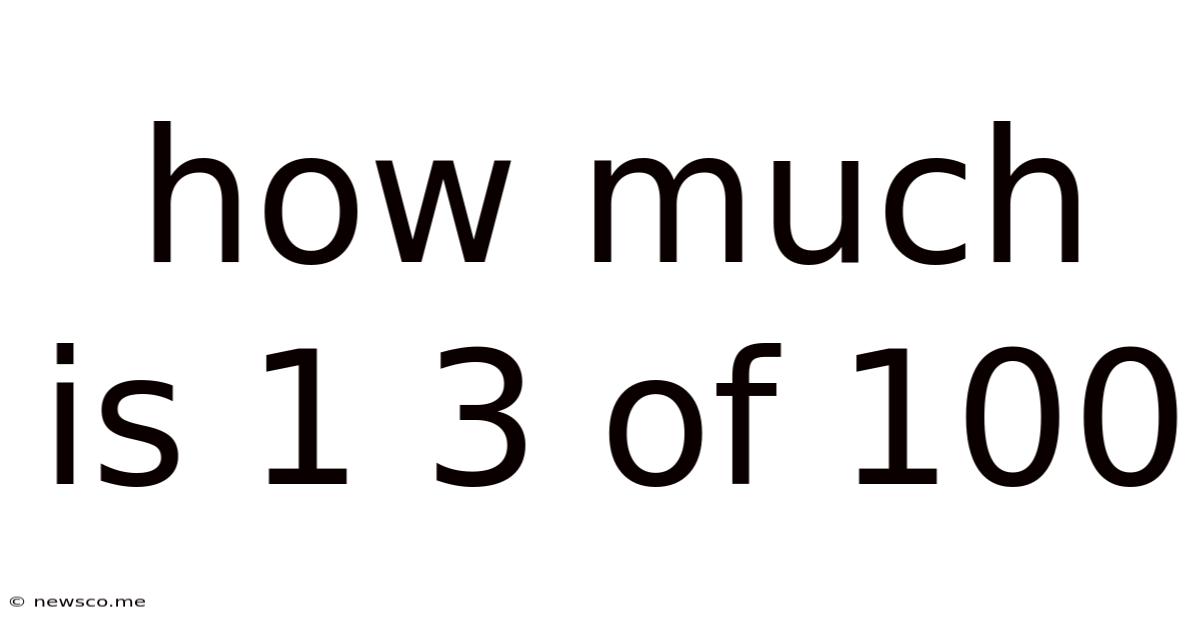
Table of Contents
How Much is 1/3 of 100? A Deep Dive into Fractions and Their Applications
Finding a fraction of a number is a fundamental concept in mathematics, crucial for various applications in everyday life, from cooking and shopping to complex scientific calculations. This article explores the simple yet vital question: How much is 1/3 of 100? We'll delve into the calculation, discuss different methods to solve it, and explore its applications across various fields. We'll also examine related concepts to solidify your understanding of fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the problem, let's quickly refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 1/3, 1 is the numerator and 3 is the denominator. This means we're considering one part out of a whole that's divided into three equal parts.
Calculating 1/3 of 100: The Simple Approach
The most straightforward way to calculate 1/3 of 100 is using multiplication. We can represent "of" as multiplication. Therefore, 1/3 of 100 can be written as:
(1/3) * 100
To perform this calculation:
- Multiply the numerator (1) by 100: 1 * 100 = 100
- Divide the result by the denominator (3): 100 / 3 = 33.333...
Therefore, 1/3 of 100 is 33.333... This is a recurring decimal, meaning the '3' repeats infinitely. For practical purposes, we often round this to 33.33 or 33 1/3.
Alternative Methods: Exploring Different Approaches
While the multiplication method is the most direct, other approaches can be equally effective, particularly for different types of fractions or when dealing with larger numbers. Let's explore a couple of alternatives:
Method 2: Division First
We can also tackle this problem by first dividing 100 into three equal parts and then taking one of those parts.
- Divide 100 by 3: 100 / 3 = 33.333...
- This gives us the value of one-third: 33.333...
This approach highlights the meaning of the fraction – dividing the whole into equal parts.
Method 3: Using Percentages
Since percentages are essentially fractions with a denominator of 100, we can convert 1/3 into a percentage to simplify the calculation.
- Convert 1/3 to a percentage: (1/3) * 100% = 33.333...%
- Find 33.333...% of 100: (33.333.../100) * 100 = 33.333...
This method provides an alternative perspective, especially useful when dealing with percentages in various contexts.
Applications of Finding Fractions: Real-World Examples
The ability to calculate fractions, such as finding 1/3 of 100, is invaluable in numerous real-world situations:
1. Cooking and Baking:
Recipes often require precise measurements. If a recipe calls for 1/3 cup of sugar for a total of 100 cookies, you'd need to calculate 1/3 of 100 to determine the amount of sugar needed for a smaller batch.
2. Shopping and Budgeting:
Imagine you want to buy a product that costs $100 and you only want to spend one-third of your money on it. You'd need to calculate 1/3 of $100 to determine how much you can spend.
3. Construction and Engineering:
In construction, accurate measurements are critical. Dividing materials into thirds or finding fractions of lengths is common in various construction projects.
4. Data Analysis and Statistics:
Understanding fractions is essential for interpreting data. For example, calculating the proportion of a sample group representing a larger population often involves working with fractions.
5. Finance and Investments:
In finance, calculations involving fractions are crucial for tasks such as calculating returns on investments, determining interest rates, and analyzing financial statements.
Beyond 1/3 of 100: Expanding Your Fraction Skills
Understanding the calculation of 1/3 of 100 provides a strong foundation for tackling more complex fractional problems. Here are some related concepts to explore:
- Improper Fractions: These are fractions where the numerator is larger than or equal to the denominator (e.g., 5/3).
- Mixed Numbers: These combine a whole number and a fraction (e.g., 1 2/3).
- Fraction Addition and Subtraction: Mastering these operations is crucial for many applications.
- Fraction Multiplication and Division: These operations are essential for solving a wider range of problems involving fractions.
- Decimal to Fraction Conversion: Understanding how to convert decimals to fractions, and vice versa, is vital for seamless calculations.
By mastering these concepts, you will significantly enhance your mathematical abilities and broaden your capacity to solve problems involving fractions in various domains.
Practical Tips for Working with Fractions
- Practice Regularly: Consistent practice is key to mastering fraction calculations. Start with simple problems and gradually progress to more complex ones.
- Visual Aids: Use visual aids like diagrams and fraction circles to visualize the concept of fractions and help you understand their meaning.
- Online Resources: Numerous online resources, including videos and interactive exercises, can help you improve your understanding and practice your skills.
- Real-world Applications: Try applying your fraction knowledge to everyday situations to reinforce your learning and build confidence.
Conclusion: Mastering Fractions for a Brighter Future
The question "How much is 1/3 of 100?" might seem simple, but it unlocks a deeper understanding of fractions and their immense value across diverse fields. From everyday tasks like cooking and shopping to sophisticated calculations in science and finance, the ability to work with fractions is an invaluable skill. By understanding the different methods for calculating fractions, expanding your knowledge of related concepts, and engaging in regular practice, you can build a strong foundation for success in mathematics and beyond. Remember, practice makes perfect, so keep working with fractions, and you'll soon find them easy and intuitive.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 1 3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.