How Much Is 2 3 Plus 2 3
News Co
Apr 07, 2025 · 4 min read
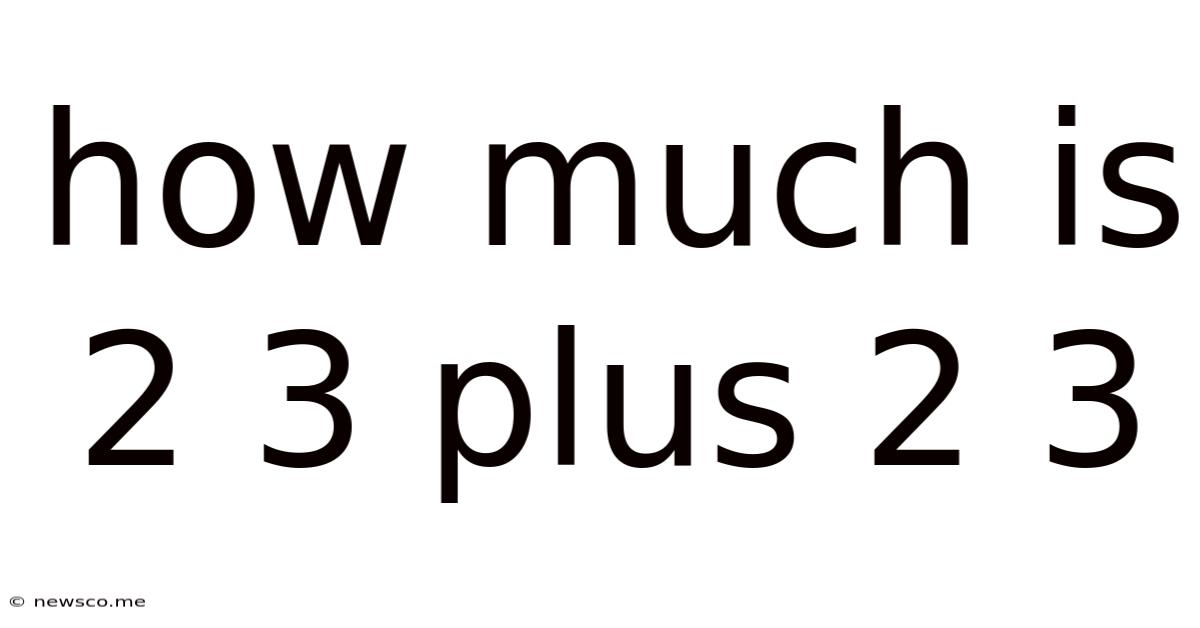
Table of Contents
How Much is 2³ + 2³? A Deep Dive into Exponents and Beyond
The seemingly simple question, "How much is 2³ + 2³?", opens a door to a fascinating exploration of mathematical concepts, from basic arithmetic to more advanced algebraic principles. While the immediate answer is easily calculated, understanding the underlying mechanics provides a strong foundation for more complex mathematical problems. This article will not only answer the question but will delve into the intricacies of exponents, their properties, and their applications in various fields.
Understanding Exponents
Before we tackle the problem, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression 2³, the number 2 is the base, and the number 3 is the exponent. This means 2³ is equivalent to 2 × 2 × 2, which equals 8.
Key Properties of Exponents
Understanding the properties of exponents is crucial for simplifying expressions and solving equations. Some key properties include:
-
Product of Powers: When multiplying two numbers with the same base, you add the exponents: a<sup>m</sup> × a<sup>n</sup> = a<sup>m+n</sup>. For example, 2² × 2³ = 2<sup>2+3</sup> = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents: a<sup>m</sup> ÷ a<sup>n</sup> = a<sup>m-n</sup>. For example, 2⁵ ÷ 2² = 2<sup>5-2</sup> = 2³ = 8.
-
Power of a Power: When raising a power to another power, you multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>. For example, (2²)³ = 2<sup>2×3</sup> = 2⁶ = 64.
-
Power of a Product: When raising a product to a power, you raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (2 × 3)² = 2² × 3² = 4 × 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. For example, (2/3)² = 2²/3² = 4/9.
Solving 2³ + 2³
Now, armed with our knowledge of exponents, we can easily solve the original problem: 2³ + 2³.
First, we calculate the value of 2³:
2³ = 2 × 2 × 2 = 8
Therefore, the expression becomes:
8 + 8 = 16
Thus, 2³ + 2³ = 16
Expanding the Concept: Applications of Exponents
The concept of exponents extends far beyond simple arithmetic. They are fundamental to various areas of mathematics and science, including:
1. Algebra
Exponents are essential in algebraic manipulations, particularly when dealing with polynomials and equations. Understanding exponent rules allows for simplification and solving of complex algebraic expressions. For example, consider expanding (x + 2)³. This requires understanding the binomial theorem and the properties of exponents.
2. Calculus
Exponents are crucial in calculus, forming the basis of exponential functions and their derivatives and integrals. Exponential functions describe growth and decay processes in numerous applications. For instance, understanding exponential growth is crucial in modeling population growth, radioactive decay, and compound interest.
3. Physics
Exponents frequently appear in physics equations. For instance, Newton's Law of Universal Gravitation uses exponents to describe the relationship between the gravitational force, masses, and distance. Similarly, many formulas in kinematics (the study of motion) involve exponents to represent acceleration, velocity, and displacement.
4. Computer Science
Exponents are fundamental in computer science, particularly in algorithm analysis. The complexity of an algorithm, which describes how its runtime scales with input size, is often expressed using Big O notation, which frequently involves exponential functions. For example, an algorithm with exponential time complexity becomes computationally infeasible for large inputs.
5. Finance
Compound interest, a cornerstone of financial mathematics, relies heavily on exponents. The formula for compound interest incorporates exponents to demonstrate the exponential growth of investments over time.
Beyond the Basics: More Complex Exponent Problems
While 2³ + 2³ is a simple problem, let's explore more complex scenarios that build upon the fundamental principles discussed.
Consider the problem: (2³ + 3²)⁴
First, we evaluate the terms inside the parentheses:
2³ = 8 3² = 9
So the expression becomes: (8 + 9)⁴ = 17⁴
Now, we calculate 17⁴:
17⁴ = 17 × 17 × 17 × 17 = 83521
Therefore, (2³ + 3²)⁴ = 83521
Let's tackle another example: Simplify 2⁵ x 2² ÷ 2³
Using the rules of exponents:
2⁵ x 2² = 2<sup>5+2</sup> = 2⁷
Then, 2⁷ ÷ 2³ = 2<sup>7-3</sup> = 2⁴ = 16
Therefore, 2⁵ x 2² ÷ 2³ = 16
Conclusion: The Power of Understanding Exponents
The seemingly simple equation 2³ + 2³ = 16 serves as a gateway to a much broader understanding of exponents and their significant role in various fields. Mastering the properties of exponents allows for the simplification of complex mathematical expressions and the solution of numerous problems across diverse disciplines. From basic arithmetic to advanced calculus, a solid grasp of exponents is an essential skill for anyone pursuing a deeper understanding of mathematics and its applications in the real world. Continued practice and exploration of more intricate problems will solidify this foundational knowledge and open doors to further mathematical discoveries. Remember, the journey of mathematical understanding is a continuous process of exploration and learning.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Much Is 2 3 Plus 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.