How To Factor X 3 2x 2 X 2
News Co
May 08, 2025 · 5 min read
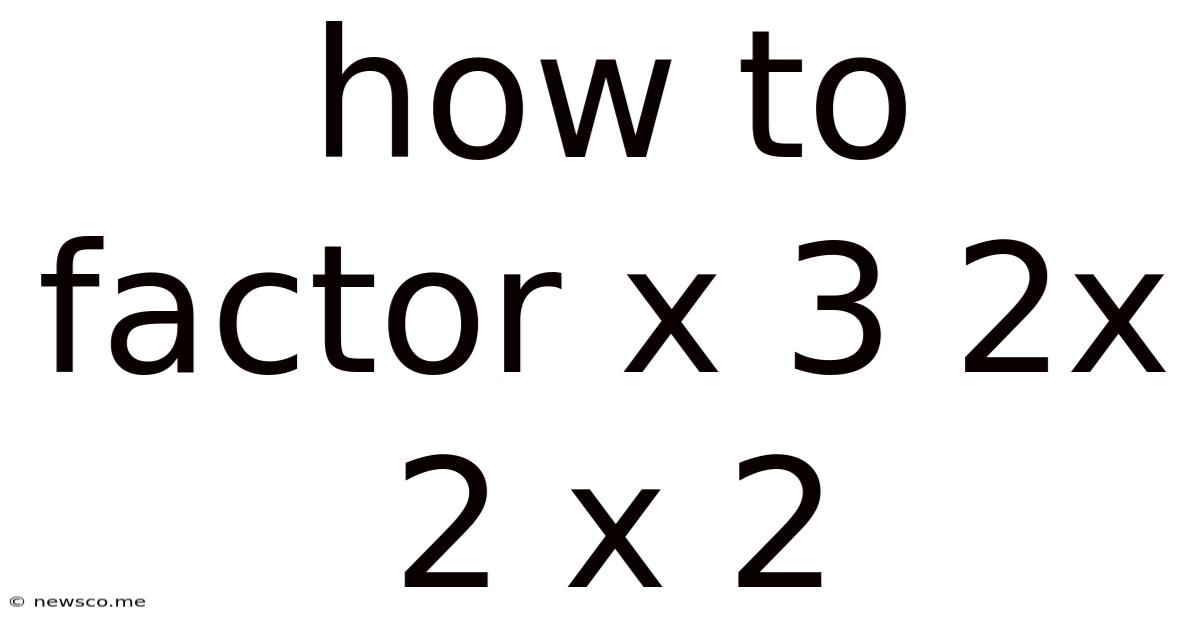
Table of Contents
How to Factor x³ + 2x² + x - 2
Factoring polynomials is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding various mathematical concepts. While simple quadratics often yield to readily apparent factoring techniques, higher-order polynomials, like the cubic expression x³ + 2x² + x - 2, require a more systematic approach. This article will guide you through various methods for factoring this specific cubic polynomial, offering a comprehensive understanding of the process and showcasing different techniques applicable to other polynomial expressions.
Understanding the Problem: x³ + 2x² + x - 2
Before diving into the solutions, let's clarify the goal. We aim to express the cubic polynomial x³ + 2x² + x - 2 as a product of simpler polynomials. Ideally, we'll find factors that are linear (degree 1) or quadratic (degree 2) expressions. The process involves finding the roots (or zeros) of the polynomial, as these roots directly relate to the factors.
Method 1: Rational Root Theorem and Polynomial Long Division
The Rational Root Theorem provides a starting point for finding rational roots of polynomials. This theorem states that any rational root of a polynomial with integer coefficients can be expressed in the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.
In our case, x³ + 2x² + x - 2:
- The constant term is -2. Its factors are ±1 and ±2.
- The leading coefficient is 1. Its factors are ±1.
Therefore, the possible rational roots are ±1 and ±2. Let's test these values by substituting them into the polynomial:
- If x = 1: 1³ + 2(1)² + 1 - 2 = 2 ≠ 0
- If x = -1: (-1)³ + 2(-1)² + (-1) - 2 = -2 ≠ 0
- If x = 2: 2³ + 2(2)² + 2 - 2 = 14 ≠ 0
- If x = -2: (-2)³ + 2(-2)² + (-2) - 2 = -8 + 8 - 2 - 2 = -4 ≠ 0
Unfortunately, none of the possible rational roots are actual roots. This doesn't mean the polynomial is prime; it just means the roots are either irrational or complex. We need to employ a different strategy. Since simple substitution didn't work, let's consider numerical methods or more advanced techniques, which are discussed in later sections.
Method 2: Graphing and Numerical Methods
A graphical approach can provide valuable insights. Plotting the function y = x³ + 2x² + x - 2 reveals the approximate location of the x-intercepts (roots) of the polynomial. Using graphing software or a graphing calculator, we can observe where the graph intersects the x-axis. These x-values represent the approximate real roots of the polynomial.
Once you have an approximation of a root (let's call it 'r'), you can use numerical methods like the Newton-Raphson method to refine the approximation to a higher degree of accuracy. This iterative method progressively refines the root's value until a desired level of precision is achieved. The process involves repeatedly applying the formula:
x_(n+1) = x_n - f(x_n) / f'(x_n)
Where:
- x_n is the current approximation of the root.
- x_(n+1) is the next, improved approximation.
- f(x_n) is the value of the polynomial at x_n.
- f'(x_n) is the value of the derivative of the polynomial at x_n.
While this method is effective, it requires knowledge of calculus (to find the derivative) and is computationally intensive if high accuracy is needed.
Method 3: Factoring by Grouping (Sometimes Applicable, but Not Here)
Factoring by grouping is a technique that sometimes works for polynomials with four or more terms. It involves grouping terms with common factors and then factoring out those common factors. However, in the case of x³ + 2x² + x - 2, this method doesn't directly lead to a factorization. Let's see why:
Attempting to group: (x³ + 2x²) + (x - 2)
Factoring out common factors: x²(x + 2) + (x - 2)
Unfortunately, we can't find a common factor between x²(x + 2) and (x - 2) to proceed further with this approach.
Method 4: Using a Computer Algebra System (CAS)
Computer Algebra Systems (CAS) like Mathematica, Maple, or symbolic calculators within programs like MATLAB are powerful tools capable of factoring complex polynomials. These programs utilize sophisticated algorithms to find the roots and factors, including irrational and complex ones. Entering the polynomial into a CAS will directly yield the factored form, eliminating the manual effort involved in the other methods.
Analyzing the Roots and Implications
Even without finding easily-identifiable rational roots, we can still draw some conclusions. The polynomial is a cubic, meaning it must have at least one real root. If we used a CAS or graphing techniques, we would find that the polynomial has one real root and two complex roots. The complex roots will always come in conjugate pairs (a + bi and a - bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit). The fact that we didn't find rational roots simply means the real root is irrational, and the complex roots have non-zero imaginary parts.
Advanced Factoring Techniques (Beyond the Scope of Simple Rational Roots)
For cubic polynomials that don't readily factor using simpler methods, more advanced techniques such as the cubic formula can be used to find the roots. However, this formula is quite complex and not usually taught at the introductory algebra level due to its cumbersome nature. Numerical methods and CAS software are often preferred for handling such cases.
Conclusion: A Multifaceted Approach to Factoring
Factoring polynomials, particularly higher-order ones like x³ + 2x² + x - 2, often requires a combined strategy. Starting with simpler methods like the Rational Root Theorem and factoring by grouping is a good first step, but if these fail, utilizing graphical analysis, numerical methods (like Newton-Raphson), or a Computer Algebra System becomes necessary. Understanding the nature of polynomial roots (real versus complex, rational versus irrational) is crucial in guiding your choice of approach and interpreting the results. The absence of easily identifiable rational roots doesn't imply that the polynomial is unfactorable; it simply means the factors are more complex and require more sophisticated tools or techniques to reveal.
Latest Posts
Latest Posts
-
What Do Two Lines Mean In Math
May 08, 2025
-
Adding Integers With The Same Sign Worksheet
May 08, 2025
-
Area And Perimeter Of A Triangle Worksheet
May 08, 2025
-
40 Bottles Of Water Is How Many Gallons
May 08, 2025
-
What Is 72 Written As A Decimal
May 08, 2025
Related Post
Thank you for visiting our website which covers about How To Factor X 3 2x 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.