How To Find Derivative Of Integral
News Co
Apr 03, 2025 · 5 min read
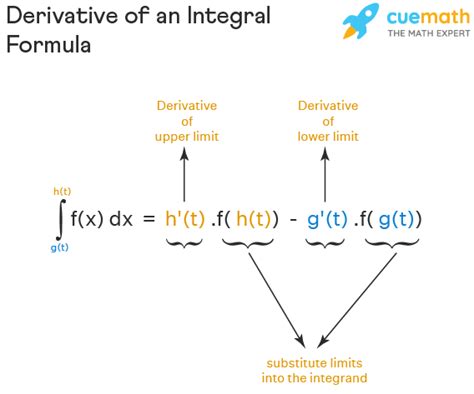
Table of Contents
How to Find the Derivative of an Integral: A Comprehensive Guide
Finding the derivative of an integral might seem counterintuitive at first – aren't derivatives and integrals opposites? While they are indeed inverse operations, understanding how they interact is crucial in calculus and its applications. This comprehensive guide will explore various methods and scenarios, equipping you with the knowledge to tackle diverse problems confidently.
Understanding the Fundamental Theorem of Calculus
The key to understanding how to find the derivative of an integral lies in the Fundamental Theorem of Calculus (FTC). This theorem connects differentiation and integration, providing a powerful tool for solving many calculus problems. The FTC has two parts, but it's the second part that directly addresses our question:
FTC Part 2: If f is continuous on [a, b], then the function F defined by
F(x) = ∫[a, x] f(t) dt
is continuous on [a, b] and differentiable on (a, b), and F'(x) = f(x) for a < x < b.
In simpler terms: If you have an integral with a variable upper limit of integration, its derivative is simply the integrand (the function inside the integral) with the variable of integration replaced by the upper limit.
Example 1: A Simple Case
Let's consider a straightforward example:
Find the derivative of:
F(x) = ∫[1, x] t² dt
According to the FTC Part 2, the derivative is simply the integrand with t replaced by x:
F'(x) = x²
This elegantly demonstrates the core principle. The integral represents the area under the curve of t² from 1 to x. The derivative, x², represents the instantaneous rate of change of this area as x changes.
Dealing with Variable Upper and Lower Limits
The FTC Part 2 directly addresses integrals with a variable upper limit and a constant lower limit. However, what happens when both limits are variables, or when the limits are functions of x?
Variable Upper and Lower Limits
Consider the integral:
G(x) = ∫[x², x] f(t) dt
We can't directly apply the FTC Part 2. Instead, we use the property of definite integrals:
∫[a, b] f(t) dt = -∫[b, a] f(t) dt
Rewrite G(x) as:
G(x) = ∫[x², x] f(t) dt = ∫[x², c] f(t) dt + ∫[c, x] f(t) dt
where c is a constant. Now we can apply the chain rule and the FTC Part 2:
G'(x) = f(x) * 1 - f(x²) * 2x
Notice the application of the chain rule due to the variable limits and that the derivative of the lower limit is multiplied by the function at that limit (with the appropriate substitution for t). This is a critical aspect when dealing with variable limits.
Variable Limits as Functions of x
Suppose we have:
H(x) = ∫[g(x), h(x)] f(t) dt
where g(x) and h(x) are differentiable functions of x. We can use the Leibniz rule for differentiation under the integral sign:
H'(x) = f(h(x))h'(x) - f(g(x))g'(x)
This formula directly incorporates the derivatives of the upper and lower limits, highlighting the chain rule's importance.
Example 2: Variable Limits
Let's find the derivative of:
I(x) = ∫[x, x³] sin(t) dt
Using the Leibniz rule:
I'(x) = sin(x³) * 3x² - sin(x) * 1 = 3x²sin(x³) - sin(x)
This clearly shows the application of the chain rule and the subtraction of the derivatives of the integrands evaluated at the lower and upper limits.
Handling More Complex Integrals
The scenarios above cover the most common cases. However, the approach can be adapted to more complex situations.
Integrals with Parameters
Sometimes, integrals might contain parameters that aren't the variable of integration. These parameters can influence the result, but the differentiation process remains similar. For instance:
J(x) = ∫[0, x] t*e^(kt) dt
Here, 'k' is a parameter. The derivative with respect to x is:
J'(x) = x * e^(kx)
The parameter k remains unchanged during differentiation; we only focus on the variable of integration.
Dealing with Discontinuities in the Integrand
The FTC requires the integrand to be continuous. If the integrand has discontinuities within the interval of integration, you might need to split the integral into separate parts, each with a continuous integrand, before applying the derivative.
Dealing with Integrals Involving Trigonometric and Exponential Functions
Applying the techniques described is applicable regardless of the form of the function.
For example:
K(x) = ∫[1, x] e^(t²) dt
The derivative is simply:
K'(x) = e^(x²)
Similarly, for trigonometric functions:
L(x) = ∫[0, x] cos(t³) dt
The derivative is:
L'(x) = cos(x³)
Practical Applications
Understanding the derivative of an integral has significant applications in various fields:
- Physics: Calculating velocity from acceleration, or displacement from velocity.
- Economics: Determining the marginal cost from a cost function.
- Engineering: Analyzing rates of change in various systems.
- Probability and Statistics: Working with probability density functions and cumulative distribution functions.
Conclusion
Finding the derivative of an integral is a fundamental concept in calculus. By mastering the Fundamental Theorem of Calculus and the techniques described – including handling variable limits, parameters, and discontinuities – you can confidently tackle a wide array of problems and unlock its powerful applications across various disciplines. Remember that practice is key; work through various examples to solidify your understanding and build your problem-solving skills. The elegance and power of the FTC, coupled with the chain rule, provide a robust and efficient method for solving these seemingly complex mathematical relationships. This deep understanding not only improves your mathematical proficiency but also opens doors to advanced topics in calculus and its practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find Derivative Of Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.