How To Find Height Of Parallelogram
News Co
Apr 05, 2025 · 5 min read
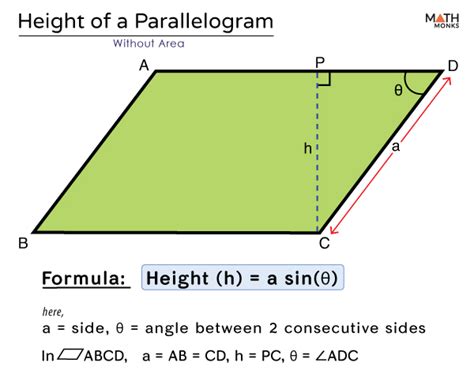
Table of Contents
How to Find the Height of a Parallelogram: A Comprehensive Guide
Finding the height of a parallelogram might seem straightforward, but understanding the nuances is crucial for accurate calculations in geometry and related fields. This comprehensive guide will delve into various methods for determining the parallelogram's height, addressing different scenarios and providing practical examples. We’ll explore both the theoretical underpinnings and the practical application of these methods, ensuring you gain a solid grasp of this fundamental geometric concept.
Understanding Parallelograms and Their Properties
Before we dive into the methods for finding the height, let's establish a firm understanding of parallelograms themselves. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. This fundamental property directly influences how we calculate its height.
Key Properties of Parallelograms:
- Opposite sides are parallel: This is the defining characteristic.
- Opposite sides are equal in length: AB = CD and BC = DA.
- Opposite angles are equal: ∠A = ∠C and ∠B = ∠D.
- Consecutive angles are supplementary: ∠A + ∠B = 180°, ∠B + ∠C = 180°, and so on.
- Diagonals bisect each other: The diagonals intersect at their midpoints.
Defining the Height of a Parallelogram
The height of a parallelogram is the perpendicular distance between two parallel sides. It's crucial to understand that the height is always perpendicular to the base. This perpendicularity is what differentiates the height from simply the length of a side. Think of it as the shortest distance between the two parallel sides.
Methods for Finding the Height of a Parallelogram
Several methods exist for determining the height, depending on the information available. Let's explore the most common approaches:
1. Using the Area and Base Length
This is perhaps the most straightforward method. The area of a parallelogram is given by the formula:
Area = base × height
If you know the area and the length of the base, you can easily solve for the height:
height = Area / base
Example:
A parallelogram has an area of 30 square centimeters and a base of 5 centimeters. What is its height?
height = 30 cm² / 5 cm = 6 cm
Therefore, the height of the parallelogram is 6 centimeters.
2. Using Trigonometry (Right-Angled Triangles)
When dealing with parallelograms where only the side lengths and angles are known, trigonometry provides a powerful tool. By constructing a right-angled triangle within the parallelogram, we can use trigonometric functions (sine, cosine, tangent) to find the height.
Example:
Consider a parallelogram with a base of 10 cm and an angle of 30° between the base and a side of length 8 cm. To find the height (h):
- We can create a right-angled triangle where the hypotenuse is 8 cm and the angle opposite the height is 30°.
- Using the sine function: sin(30°) = h / 8 cm
- Solving for h: h = 8 cm * sin(30°) = 8 cm * 0.5 = 4 cm
Therefore, the height of the parallelogram is 4 centimeters.
This method can be adapted for different scenarios depending on the known angles and side lengths. Remember that the choice of trigonometric function (sin, cos, tan) depends on which sides and angles are known.
3. Using Coordinate Geometry
If the vertices of the parallelogram are given as coordinates in a Cartesian plane, we can use the distance formula and the concept of the slope of a line to determine the height.
Steps:
- Find the equation of the base: Using two points on the base, find the equation of the line representing the base.
- Find the equation of the height: The height is perpendicular to the base. Therefore, the slope of the height is the negative reciprocal of the slope of the base. Using a point on the base and the slope of the height, find the equation of the line representing the height.
- Find the intersection point: Solve the system of equations formed by the equations of the base and the height. This gives you the coordinates of the point where the height intersects the base.
- Calculate the height: Use the distance formula to find the distance between the point of intersection and the opposite vertex of the parallelogram. This distance is the height.
This method is more complex but offers a precise calculation when coordinate information is available.
4. Using Vector Methods
For those familiar with vectors, this method offers an elegant solution. The height can be found by projecting a vector representing one side of the parallelogram onto a vector representing the base. The magnitude of the projection vector is the height.
The specifics of this method involve vector dot products and normalization. It's a more advanced technique typically used in higher-level mathematics and physics.
Practical Applications of Finding Parallelogram Height
Understanding how to find the height of a parallelogram has numerous real-world applications:
- Engineering: Calculating areas of building foundations, land plots, or other structures with parallelogram shapes.
- Architecture: Designing roofs, walls, and other architectural elements that utilize parallelogram shapes.
- Physics: Determining force components in physics problems involving parallelogram-shaped objects.
- Graphic Design: Precise layout of design elements within parallelogram shapes.
- Cartography: Calculating areas on maps involving parallelograms.
Common Mistakes to Avoid
- Confusing height with side length: Remember, the height is the perpendicular distance, not simply the length of a side.
- Incorrectly applying trigonometric functions: Ensure you're using the correct trigonometric function (sin, cos, tan) based on the available information.
- Errors in coordinate geometry calculations: Carefully perform distance and slope calculations to minimize error.
Conclusion
Finding the height of a parallelogram is a fundamental geometric skill with broad applications. By mastering the various methods outlined in this guide, you'll be well-equipped to handle various scenarios, from simple calculations using area and base length to more complex methods involving trigonometry or coordinate geometry. Remember that understanding the properties of parallelograms is crucial for accurate calculations, and always double-check your work to ensure accuracy. This guide provides a complete and thorough understanding of how to effectively determine the height of a parallelogram, equipping you with the knowledge needed for various applications in numerous fields. The combination of theoretical explanations and practical examples ensures a comprehensive learning experience. Remember to always consider the specific information you have available when selecting the most appropriate method for solving a problem.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find Height Of Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.