How To Find Lateral Area Of A Cone
News Co
Apr 05, 2025 · 6 min read
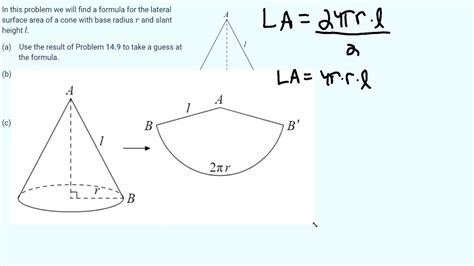
Table of Contents
How to Find the Lateral Surface Area of a Cone: A Comprehensive Guide
Understanding how to calculate the lateral surface area of a cone is crucial in various fields, from engineering and architecture to advanced mathematics. This comprehensive guide will equip you with the knowledge and formulas to confidently tackle this geometrical challenge. We'll explore the concept, delve into the formulas, and work through examples to solidify your understanding. This guide also incorporates relevant SEO keywords throughout the text to enhance searchability.
Understanding the Cone and its Lateral Surface Area
A cone is a three-dimensional geometric shape characterized by a circular base and a single apex point directly above the center of the base. Imagine an ice cream cone – the circular waffle is the base, and the pointed top is the apex. The lateral surface area refers to the curved surface of the cone, excluding the circular base. It's the area you'd paint if you were only painting the cone's sloped sides. The total surface area, on the other hand, includes both the lateral surface area and the area of the circular base.
Key Components of a Cone:
- Radius (r): The radius is the distance from the center of the circular base to any point on the edge of the circle.
- Slant Height (l): The slant height is the distance from the apex of the cone to any point on the circumference of the base. It's not the height of the cone (which we'll discuss later). It's the distance along the cone's curved surface.
- Height (h): The height is the perpendicular distance from the apex to the center of the circular base.
These components are interconnected and crucial for calculating the lateral surface area. Understanding their relationships is key to mastering cone calculations.
The Formula for Lateral Surface Area of a Cone
The formula for calculating the lateral surface area (LSA) of a cone is elegantly simple:
LSA = πrl
Where:
- π (pi): The mathematical constant, approximately 3.14159.
- r: The radius of the circular base.
- l: The slant height of the cone.
This formula essentially calculates the area of a sector of a circle with radius equal to the cone's slant height. Unrolling the cone's lateral surface would reveal this sector.
Calculating Slant Height (l) if only Radius (r) and Height (h) are known.
Often, you won't be directly given the slant height. Instead, you might know the radius (r) and the height (h) of the cone. In such cases, you can use the Pythagorean theorem to find the slant height:
l² = r² + h²
Therefore, l = √(r² + h²)
This formula arises from the right-angled triangle formed by the radius, height, and slant height of the cone. The slant height is the hypotenuse of this triangle.
Step-by-Step Guide to Calculating Lateral Surface Area
Let's break down the process with a step-by-step guide:
-
Identify the known values: Determine the radius (r) and the slant height (l) of the cone. If only the radius and height (h) are given, calculate the slant height (l) using the Pythagorean theorem: l = √(r² + h²)
-
Apply the formula: Substitute the values of 'r' and 'l' into the lateral surface area formula: LSA = πrl
-
Calculate: Perform the calculation using a calculator or by hand, ensuring you use the appropriate value of π (3.14159 or the value provided in the problem).
-
State the answer: Remember to include the appropriate units (e.g., square centimeters, square meters, square inches) in your final answer. Clearly state that your answer represents the lateral surface area.
Examples: Putting it into Practice
Let's solidify our understanding with a few examples:
Example 1:
A cone has a radius of 5 cm and a slant height of 13 cm. Find its lateral surface area.
-
Known values: r = 5 cm, l = 13 cm
-
Formula: LSA = πrl
-
Calculation: LSA = π * 5 cm * 13 cm = 65π cm² ≈ 204.2 cm²
-
Answer: The lateral surface area of the cone is approximately 204.2 square centimeters.
Example 2:
A cone has a radius of 3 meters and a height of 4 meters. Find its lateral surface area.
-
Calculate slant height: l = √(r² + h²) = √(3² + 4²) = √(9 + 16) = √25 = 5 meters
-
Known values: r = 3 meters, l = 5 meters
-
Formula: LSA = πrl
-
Calculation: LSA = π * 3 meters * 5 meters = 15π m² ≈ 47.1 m²
-
Answer: The lateral surface area of the cone is approximately 47.1 square meters.
Example 3: A Real-World Application
Imagine you're designing a conical water tank. You know the tank's radius is 2 feet and its height is 6 feet. To determine the amount of material needed for the tank's curved surface (excluding the base), you need to calculate the lateral surface area.
-
Calculate slant height: l = √(r² + h²) = √(2² + 6²) = √40 feet
-
Known values: r = 2 feet, l = √40 feet
-
Formula: LSA = πrl
-
Calculation: LSA = π * 2 feet * √40 feet ≈ 39.7 square feet
-
Answer: Approximately 39.7 square feet of material is needed for the curved surface of the water tank.
Advanced Concepts and Related Calculations
While the basic formula for lateral surface area is straightforward, several advanced concepts build upon this foundation:
-
Frustum of a cone: A frustum is the portion of a cone remaining after its top is cut off by a plane parallel to its base. Calculating the lateral surface area of a frustum requires a slightly modified formula.
-
Curved surface area with more complex shapes: The principle of calculating the curved surface area can be extended to other three-dimensional shapes involving curved surfaces.
-
Using calculus for irregular cones: For cones with irregularly shaped bases, calculus techniques (surface integrals) become necessary to accurately determine the lateral surface area.
Troubleshooting Common Mistakes
-
Confusing slant height and height: Remember that the slant height (l) is the distance along the curved surface, not the perpendicular height (h) from the apex to the base.
-
Incorrect unit conversion: Ensure consistent units throughout the calculation. If your radius is in centimeters, your slant height must also be in centimeters, and your final answer will be in square centimeters.
-
Using the wrong formula: Double-check that you are using the correct formula for lateral surface area (πrl) and not confusing it with the formula for total surface area or volume.
By understanding the fundamental formula, practicing with examples, and being mindful of common pitfalls, you'll master the calculation of the lateral surface area of a cone with confidence. This skill will prove invaluable in various academic and practical applications. Remember to always clearly label your answers with the correct units and specify that the answer represents the lateral surface area.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find Lateral Area Of A Cone . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.