How To Find The Base Of Triangular Prism
News Co
Apr 07, 2025 · 6 min read
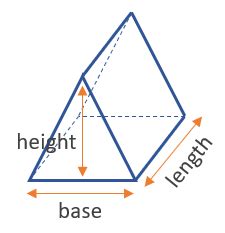
Table of Contents
How to Find the Base of a Triangular Prism: A Comprehensive Guide
Finding the base of a triangular prism might seem straightforward, but a deeper understanding is crucial for various applications, from calculating volume and surface area to tackling more complex geometrical problems. This comprehensive guide delves into the intricacies of identifying and understanding the base of a triangular prism, catering to diverse levels of mathematical proficiency. We'll cover different scenarios, common misconceptions, and practical examples to solidify your understanding.
Understanding Triangular Prisms: A Foundation
Before diving into base identification, let's establish a firm grasp of what constitutes a triangular prism. A triangular prism is a three-dimensional geometric shape characterized by:
- Two congruent triangular faces: These are the bases of the prism. They are identical in shape and size and are parallel to each other.
- Three rectangular faces: These faces connect the two triangular bases. Their dimensions are determined by the sides of the triangular bases and the height of the prism.
The key takeaway is that the bases are always the parallel congruent triangular faces. This is fundamental to all calculations involving the prism.
Identifying the Base: Common Scenarios and Approaches
Identifying the base often depends on how the triangular prism is presented. Let's explore several common scenarios and the strategies to confidently pinpoint the bases:
1. The Prism is Oriented "Upright":
This is the most intuitive scenario. The prism is positioned with its triangular faces parallel to the horizontal plane. In this case, the two triangular faces are clearly identifiable as the bases. There's no ambiguity; they are parallel, congruent, and form the top and bottom of the prism.
Example: Imagine a triangular prism sitting on a table. The triangle touching the table is one base; the other triangle forms the top face.
2. The Prism is Lying on One of its Rectangular Faces:
This is where careful observation is key. While the prism might appear different, the fundamental characteristic remains: the bases are still the two parallel congruent triangular faces. You need to mentally rotate or visualize the prism to identify the parallel triangles. Look for the two congruent triangles that are parallel to each other, regardless of their orientation relative to the ground.
Example: Imagine the same prism lying on one of its rectangular sides. Even though a rectangle forms the bottom face, the two triangular faces remain parallel and congruent, and thus are the bases.
3. The Prism is Presented in a Diagram or Drawing:
Diagrams can sometimes be deceptive. Pay close attention to the following:
- Parallelism: Check for the presence of two parallel triangular faces. This is the defining characteristic of the bases.
- Congruence: Verify if the two identified triangles are congruent. They must have identical side lengths and angles.
- Labels: Diagrams sometimes clearly label the bases. Look for any markings or notations indicating the bases.
If the diagram is unclear, redrawing it from a different perspective may help clarify the orientation and identify the bases more easily.
4. The Prism is Described in a Problem Statement:
Word problems often describe the dimensions of the prism indirectly. Carefully read the description, paying close attention to the following:
- Triangular faces: Look for mentions of "triangular ends" or "triangular faces". These are strong indicators of the bases.
- Dimensions of the triangles: If the problem provides dimensions (side lengths, angles, etc.) for two triangles, and these dimensions are identical, those two triangles are the bases.
- Height: The problem might mention the height of the prism, usually referring to the perpendicular distance between the two triangular bases.
By carefully analyzing the textual description, you can deduce which faces serve as the bases.
Common Misconceptions and Pitfalls
Several misconceptions can lead to inaccurate base identification. Let's address some common errors:
- Confusing Bases with Rectangular Faces: The most frequent mistake is assuming the rectangular faces are the bases. Remember, the bases are always the congruent, parallel triangular faces.
- Ignoring Parallelism: Focusing solely on congruence without considering parallelism can lead to incorrect identification. Both parallelism and congruence are essential.
- Misinterpreting Diagrams: Incorrect perspective in a diagram can make identification challenging. Always verify parallelism and congruence even if the diagram seems obvious.
- Overlooking Implicit Information: Word problems may not explicitly state "bases," requiring careful deduction from the given information.
Avoiding these pitfalls requires careful attention to the defining properties of triangular prisms and a methodical approach to identification.
Practical Applications: Calculations and Problem Solving
Once you have correctly identified the base, you can proceed with various calculations:
1. Calculating the Area of the Base:
The area of the triangular base is crucial for calculating the volume and surface area of the prism. The method used depends on the information available:
- If side lengths are known (Heron's Formula): Use Heron's formula, which is applicable to any triangle: Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter (s = (a+b+c)/2) and a, b, and c are the side lengths.
- If base and height are known: Use the simple formula: Area = (1/2) * base * height. This is the most straightforward approach when the base and height of the triangle are given.
2. Calculating the Volume of the Triangular Prism:
The volume is given by: Volume = Area of Base * Height of Prism. The "height of the prism" refers to the perpendicular distance between the two triangular bases.
3. Calculating the Surface Area of the Triangular Prism:
The surface area involves calculating the area of all faces – the two triangular bases and the three rectangular faces. The formula is: Surface Area = 2 * Area of Base + Area of Rectangle 1 + Area of Rectangle 2 + Area of Rectangle 3. The area of each rectangle is calculated by multiplying its length and width.
Advanced Scenarios and Considerations
Let's explore some more complex situations:
1. Oblique Triangular Prisms:
In an oblique triangular prism, the rectangular faces are not perpendicular to the bases. While the identification of the bases remains the same (the two parallel congruent triangles), calculating the volume and surface area requires slightly different approaches using vector methods or trigonometry.
2. Irregular Triangular Prisms:
If the triangular bases are irregular (i.e., no sides are equal), the area calculations become more involved, often requiring the use of trigonometry or coordinate geometry. However, the identification of the bases remains unchanged: they are still the two parallel congruent triangular faces.
Conclusion: Mastering Base Identification and Beyond
Accurately identifying the base of a triangular prism is paramount to successful geometrical problem-solving. By understanding the defining properties – parallelism and congruence of the triangular faces – and by avoiding common misconceptions, you can confidently navigate various scenarios, from straightforward visualizations to more complex problems involving oblique or irregular prisms. Mastering this fundamental concept opens the door to a deeper understanding of three-dimensional geometry and its applications in various fields. Remember to always practice, utilizing a variety of problems and approaches to solidify your understanding and build your confidence in handling these geometrical challenges. The journey to mastering triangular prisms starts with a strong foundation in base identification.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find The Base Of Triangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.