How To Find The Height Of A Trapezoid Without Area
News Co
Apr 05, 2025 · 6 min read
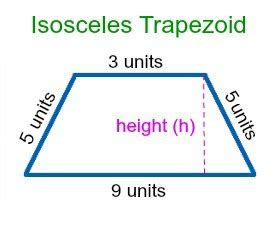
Table of Contents
How to Find the Height of a Trapezoid Without the Area
Finding the height of a trapezoid without knowing its area might seem impossible at first glance. After all, the standard area formula for a trapezoid directly incorporates the height. However, several methods exist, depending on the information you already possess about the trapezoid. This comprehensive guide will explore various scenarios and techniques to determine the trapezoid's height without relying on the area calculation.
Understanding the Trapezoid and its Properties
Before diving into the methods, let's refresh our understanding of a trapezoid. A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases (often denoted as 'b1' and 'b2'), while the non-parallel sides are called legs. The height (h) of a trapezoid is the perpendicular distance between the two parallel bases.
This seemingly simple geometric shape can present various challenges when trying to determine its height without the area. The key is to leverage other properties and relationships within the trapezoid, often involving trigonometry or the Pythagorean theorem.
Methods to Find the Height of a Trapezoid Without Area
The method you choose will depend entirely on the information provided. Here are several scenarios and their corresponding solutions:
1. Using the Legs and Base Angles
If you know the lengths of the two legs (let's call them 'a' and 'c') and the angles they make with the bases (let's say angles α and β, where α is the angle between leg 'a' and base 'b1' and β is the angle between leg 'c' and base 'b2'), you can use trigonometry to find the height.
Steps:
-
Draw perpendiculars: Draw perpendicular lines from the endpoints of the shorter base to the longer base. This divides the trapezoid into a rectangle and two right-angled triangles.
-
Trigonometric application: The height (h) of the trapezoid is the same as the height of the two right-angled triangles. You can use trigonometric functions (sine or cosine) to find the height. Consider the triangle formed by leg 'a', the base segment adjacent to it, and the height. You can express the height as:
h = a * sin(α)
Similarly, using the other triangle:
h = c * sin(β)
-
Verification: Since both equations give the height, they can be used to verify the result. Discrepancies might indicate an error in the given angles or leg lengths.
Example:
Let's say a = 5 units, c = 7 units, α = 30°, and β = 45°.
h = 5 * sin(30°) = 5 * 0.5 = 2.5 unitsh = 7 * sin(45°) = 7 * 0.707 ≈ 4.95 units
Notice the discrepancy. This suggests a problem in the data provided. The angles and leg lengths must be consistent with a valid trapezoid.
2. Using the Bases and the Length of the Non-parallel Sides
If you know the lengths of both bases (b1 and b2) and one of the non-parallel sides (let's say 'a'), along with the angle it forms with the base (θ), you can again use trigonometry to find the height.
Steps:
-
Construct a right-angled triangle: Extend the shorter base until it intersects with the leg a, creating a right-angled triangle.
-
Find the base of the triangle: The base of this right-angled triangle will be (b2 - b1).
-
Trigonometric calculation: Use trigonometric functions to find the height (h). In this case, using the tangent function:
tan(θ) = h / (b2 - b1)h = (b2 - b1) * tan(θ)
Example:
Suppose b1 = 4 units, b2 = 10 units, a = 6 units, and θ = 60°. The difference between the bases is 6 units.
h = 6 * tan(60°) = 6 * √3 ≈ 10.39 units
3. Using Coordinates of Vertices
If the vertices of the trapezoid are given as Cartesian coordinates (x, y), you can find the height by calculating the perpendicular distance between the parallel bases.
Steps:
-
Identify the parallel bases: Determine which two sides are parallel.
-
Find the equation of the line: Find the equation of the line that contains one of the parallel bases.
-
Calculate the distance: Use the formula for the distance between a point and a line to calculate the perpendicular distance from any point on the other parallel base to the line found in step 2. This distance is the height of the trapezoid.
This method involves some algebra but is relatively straightforward, particularly if you're comfortable with coordinate geometry.
4. Isosceles Trapezoid with Legs and Bases
If the trapezoid is an isosceles trapezoid (meaning the two non-parallel sides are equal in length), and you know the lengths of the bases (b1 and b2) and the length of one leg (a), you can solve it using the Pythagorean theorem.
Steps:
-
Construct a right triangle: Drop perpendiculars from the endpoints of the shorter base to the longer base. This creates two congruent right-angled triangles and a rectangle in the middle.
-
Find the base of the right triangle: The base of the right-angled triangle will be half the difference between the two bases:
(b2 - b1) / 2 -
Apply Pythagorean Theorem: Use the Pythagorean theorem (a² = b² + c²) to solve for the height (h):
h² + ((b2 - b1) / 2)² = a²h = √(a² - ((b2 - b1) / 2)²)
Example:
Let’s say b1 = 4, b2 = 10, and a = 5.
h = √(5² - ((10 - 4) / 2)²) = √(25 - 9) = √16 = 4 units
Important Considerations and Potential Challenges
-
Data Accuracy: The accuracy of the calculated height depends heavily on the accuracy of the input data (lengths of sides, angles, coordinates). Slight errors in the input can lead to significant errors in the output.
-
Ambiguity: In some cases, the given information might not be sufficient to uniquely determine the height. For instance, knowing only the lengths of the bases and one leg does not uniquely define the trapezoid.
-
Computational Tools: For complex scenarios or to verify calculations, utilizing mathematical software or online calculators can be beneficial.
-
Practical Applications: Determining the height of a trapezoid without the area is crucial in various fields, such as surveying, engineering, and architecture, where direct area measurement might be impossible or impractical.
Conclusion: Choosing the Right Approach
Finding the height of a trapezoid without its area requires a careful analysis of the available information and a strategic application of geometric principles, primarily trigonometry and the Pythagorean theorem. The method you employ will be dictated by the specific details provided. Remember to double-check your calculations and consider using computational tools to aid in complex scenarios. By mastering these techniques, you can effectively tackle various geometric problems involving trapezoids. The key is to break down the problem into smaller, manageable parts and leverage the relationships between the different components of the trapezoid. Understanding the properties of different types of trapezoids, such as isosceles trapezoids, can also significantly simplify the calculation process.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find The Height Of A Trapezoid Without Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.