How To Find The Perimeter Of A Kite
News Co
Apr 03, 2025 · 5 min read
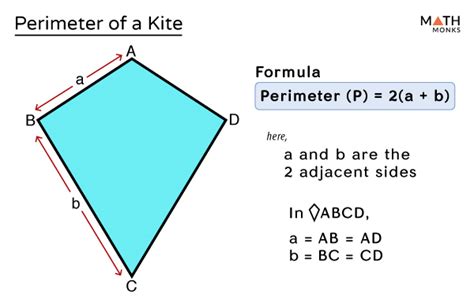
Table of Contents
How to Find the Perimeter of a Kite: A Comprehensive Guide
Understanding how to calculate the perimeter of a kite is a fundamental concept in geometry with practical applications in various fields. This comprehensive guide will delve into the intricacies of kite perimeters, equipping you with the knowledge and skills to confidently tackle any problem involving this fascinating quadrilateral. We'll explore different approaches, provide illustrative examples, and address common misconceptions. Let's embark on this geometrical journey!
What is a Kite?
Before we dive into perimeter calculations, it's crucial to have a firm grasp of what defines a kite. A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. This means that two sides next to each other are congruent, and the other two adjacent sides are also congruent. Importantly, these congruent sides are not opposite each other. This unique characteristic distinguishes kites from other quadrilaterals like squares, rectangles, rhombuses, and parallelograms.
Think of a kite as a typical flying kite – it has two pairs of equal-length sticks forming its framework. This visual analogy helps solidify the understanding of a kite's defining properties.
Key Properties of Kites: Beyond the Definition
While the definition of a kite focuses on its side lengths, understanding other properties will further enhance our ability to solve perimeter problems and approach geometry problems more strategically. These properties include:
- Two pairs of congruent adjacent sides: As mentioned earlier, this is the fundamental property defining a kite.
- One pair of opposite angles are congruent: The angles formed by the two pairs of equal sides are equal to each other.
- Diagonals intersect at right angles: The lines connecting opposite vertices (corners) of the kite meet at a 90-degree angle.
- One diagonal bisects the other: One diagonal is cut exactly in half by the other.
- Only one diagonal is a line of symmetry: The kite is symmetric about only one of its diagonals (the one that bisects the other).
Understanding these additional properties isn't strictly necessary for perimeter calculations, but they provide valuable insight into the nature of kites and can be helpful in more complex geometric problems involving kites.
How to Calculate the Perimeter of a Kite
The perimeter of any polygon, including a kite, is simply the total length of its sides. Since a kite has four sides, its perimeter is the sum of the lengths of its four sides. Let's denote the lengths of the sides as a, a, b, and b (remembering that adjacent sides are equal).
The formula for the perimeter (P) of a kite is:
P = 2a + 2b
Where:
- a represents the length of one pair of congruent adjacent sides.
- b represents the length of the other pair of congruent adjacent sides.
This formula provides a straightforward and efficient method to calculate the perimeter. Simply measure or determine the lengths of the two distinct side lengths and plug them into the equation.
Examples: Calculating Kite Perimeters
Let's solidify our understanding with a few examples:
Example 1: Simple Kite
Imagine a kite with sides of length 5 cm and 7 cm.
Using the formula:
P = 2a + 2b = 2(5 cm) + 2(7 cm) = 10 cm + 14 cm = 24 cm
Therefore, the perimeter of this kite is 24 cm.
Example 2: Kite with Variable Side Lengths
Consider a kite where one pair of adjacent sides has length 'x' and the other pair has length 'x + 3'. The perimeter is 34 units. Let's find the value of 'x'.
We know that P = 2a + 2b = 34. Substituting the values, we get:
2(x) + 2(x + 3) = 34
2x + 2x + 6 = 34
4x = 28
x = 7
Therefore, one pair of sides has length 7 units and the other pair has length 10 units (7 + 3).
Example 3: Real-World Application – Designing a Kite
You're designing a kite for a kite festival. You want the perimeter to be 48 inches. You have already decided that one pair of adjacent sides will be 10 inches long. What should the length of the other pair of sides be?
Let 'x' be the length of the other pair of sides. The equation becomes:
2(10 inches) + 2x = 48 inches
20 inches + 2x = 48 inches
2x = 28 inches
x = 14 inches
Therefore, the other pair of sides should be 14 inches long.
Dealing with Missing Information
Sometimes, you might encounter problems where you don't have the direct lengths of all sides. In such cases, you might need to employ additional geometric principles or techniques. For example:
-
Using the Pythagorean Theorem: If you know the lengths of the diagonals and need to find the side lengths, you can use the Pythagorean theorem to calculate the side lengths of the right-angled triangles formed by the diagonals. Remember that the diagonals of a kite are perpendicular.
-
Using Trigonometry: In more complex scenarios, trigonometric functions like sine, cosine, and tangent might be necessary if you have angle measures along with some side lengths.
Common Mistakes to Avoid
While calculating the perimeter of a kite is relatively straightforward, here are some common mistakes to avoid:
-
Adding all sides without considering congruent pairs: Remember that a kite has two pairs of equal sides. Simply adding four different numbers will result in an incorrect perimeter.
-
Misunderstanding the meaning of adjacent sides: Adjacent sides are those that share a common vertex (corner). Ensure you correctly identify the pairs of congruent sides.
-
Incorrectly applying other geometric theorems: While using the Pythagorean theorem or trigonometry can be helpful, make sure to apply them correctly and ensure the resulting side lengths are appropriately used in the perimeter formula.
Conclusion
Calculating the perimeter of a kite is a fundamental skill in geometry. By understanding the defining properties of kites and applying the simple formula P = 2a + 2b, you can confidently determine the perimeter of any kite, regardless of the context or information provided. Remember to double-check your work and avoid common pitfalls to ensure accuracy. This understanding forms a solid foundation for tackling more complex geometric problems involving kites and other quadrilaterals. Mastering this concept opens doors to further exploration of geometric principles and their applications in various fields. Practice makes perfect, so keep solving problems and sharpening your skills!
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find The Perimeter Of A Kite . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.