How To Find The Position Vector
News Co
Apr 07, 2025 · 5 min read
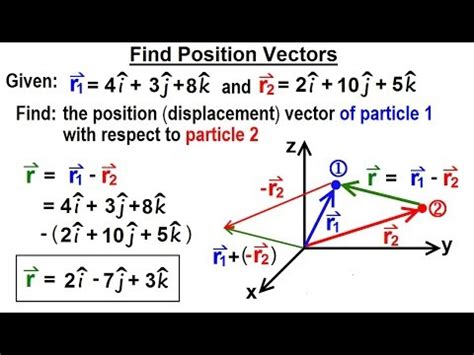
Table of Contents
How to Find the Position Vector: A Comprehensive Guide
Finding the position vector is a fundamental concept in physics and mathematics, particularly in areas like mechanics, linear algebra, and computer graphics. Understanding how to calculate and interpret position vectors is crucial for solving a wide array of problems. This comprehensive guide will delve into the intricacies of position vectors, providing you with a step-by-step approach and numerous examples to solidify your understanding.
What is a Position Vector?
A position vector, often denoted as r or x, is a vector that represents the location of a point in space relative to a reference point, usually the origin (0, 0, 0) in a Cartesian coordinate system. It essentially points from the origin to the point in question. This vector's magnitude represents the distance of the point from the origin, while its direction indicates the orientation of the point relative to the origin.
Think of it like giving directions. Instead of saying "walk 5 blocks north and then 3 blocks east," you could describe the final location with a single vector pointing directly from the starting point (origin) to the destination.
Key Components of a Position Vector
A position vector in three-dimensional space is typically represented as:
r = xi + yj + zk
Where:
- r is the position vector.
- x, y, and z are the coordinates of the point in the Cartesian coordinate system (x-axis, y-axis, and z-axis respectively).
- i, j, and k are the unit vectors along the x, y, and z axes, respectively. These vectors have a magnitude of 1 and point in the direction of their respective axes.
In two-dimensional space, the z-component is omitted:
r = xi + yj
How to Find the Position Vector: Different Scenarios
The method for finding a position vector depends on the information provided. Let's explore several scenarios:
1. Given the Coordinates of a Point
This is the most straightforward case. If you know the coordinates (x, y, z) of a point in space, you can directly construct the position vector:
Example: Find the position vector of the point P(2, 3, 4).
Solution:
The position vector r is simply:
r = 2i + 3j + 4k
2. Given Two Points: Finding the Displacement Vector
Sometimes, you might be given two points, and you need to find the position vector of one point relative to the other. This involves calculating the displacement vector.
Example: Find the position vector of point B(5, 2, 1) relative to point A(1, 0, -1).
Solution:
The displacement vector from A to B is found by subtracting the coordinates of A from the coordinates of B:
Δr = (5 - 1)i + (2 - 0)j + (1 - (-1))k = 4i + 2j + 2k
This displacement vector represents the position vector of B relative to A. If you want the position vector of B relative to the origin, you would need the coordinates of A relative to the origin. Suppose the position vector of A relative to the origin is r<sub>A</sub> = 1i - 1k. Then the position vector of B relative to the origin is r<sub>B</sub> = r<sub>A</sub> + Δr = 5i + 2j + 1k.
3. Given Magnitude and Direction
In some situations, the magnitude (length) and direction of the position vector are known. We can use trigonometry to find the components.
Example: A point is located 5 units away from the origin at an angle of 30 degrees with respect to the positive x-axis in the xy-plane. Find its position vector.
Solution:
The magnitude is 5 units. Using trigonometry:
x = 5 * cos(30°) = 5 * (√3/2) y = 5 * sin(30°) = 5 * (1/2) = 2.5 z = 0 (since it lies in the xy-plane)
Therefore, the position vector is:
r = (5√3/2)i + 2.5j
4. Using Parametric Equations
In more complex scenarios, especially in curves and motion, position vectors might be described using parametric equations. These equations express the x, y, and z coordinates as functions of a parameter (often time, denoted as 't').
Example: The position of a particle is given by the parametric equations x = 2t, y = t², z = 0. Find the position vector at t = 2.
Solution:
Substitute t = 2 into the parametric equations:
x = 2(2) = 4 y = (2)² = 4 z = 0
The position vector at t = 2 is:
r = 4i + 4j
Applications of Position Vectors
Position vectors are fundamental in many fields:
- Physics: Describing the position and motion of objects. Calculating velocities and accelerations. Analyzing forces acting on objects.
- Computer Graphics: Representing points and objects in 3D space. Performing transformations like rotations and translations. Rendering realistic images.
- Engineering: Modeling structures and mechanisms. Analyzing stresses and strains. Simulating movement.
- Navigation: Tracking the location of vehicles and aircraft.
- Robotics: Controlling the movement and position of robotic arms and manipulators.
Advanced Concepts
Unit Vector in the Direction of a Position Vector
The unit vector in the direction of a position vector r is found by dividing the position vector by its magnitude:
û = r / |r|
where |r| is the magnitude (length) of the vector r, calculated using the Pythagorean theorem:
|r| = √(x² + y² + z²)
Position Vectors and Linear Combinations
Position vectors can be combined linearly. This is useful when dealing with multiple points or when analyzing the effects of multiple forces. For instance, if you have two points A and B with position vectors r<sub>A</sub> and r<sub>B</sub>, the position vector of a point C located at the midpoint of the line segment AB can be found as:
r<sub>C</sub> = (r<sub>A</sub> + r<sub>B</sub>)/2
Conclusion
Understanding how to find the position vector is crucial for various applications across different disciplines. This guide has provided a comprehensive overview, encompassing different scenarios and methodologies. Remember to always clearly define your coordinate system and pay attention to the reference point when working with position vectors. Practice with various examples to solidify your understanding and build your problem-solving skills. By mastering this concept, you'll be well-equipped to tackle more complex problems involving vectors and spatial relationships.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Find The Position Vector . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.