How To Integrate 1 1 X 2
News Co
Mar 20, 2025 · 5 min read
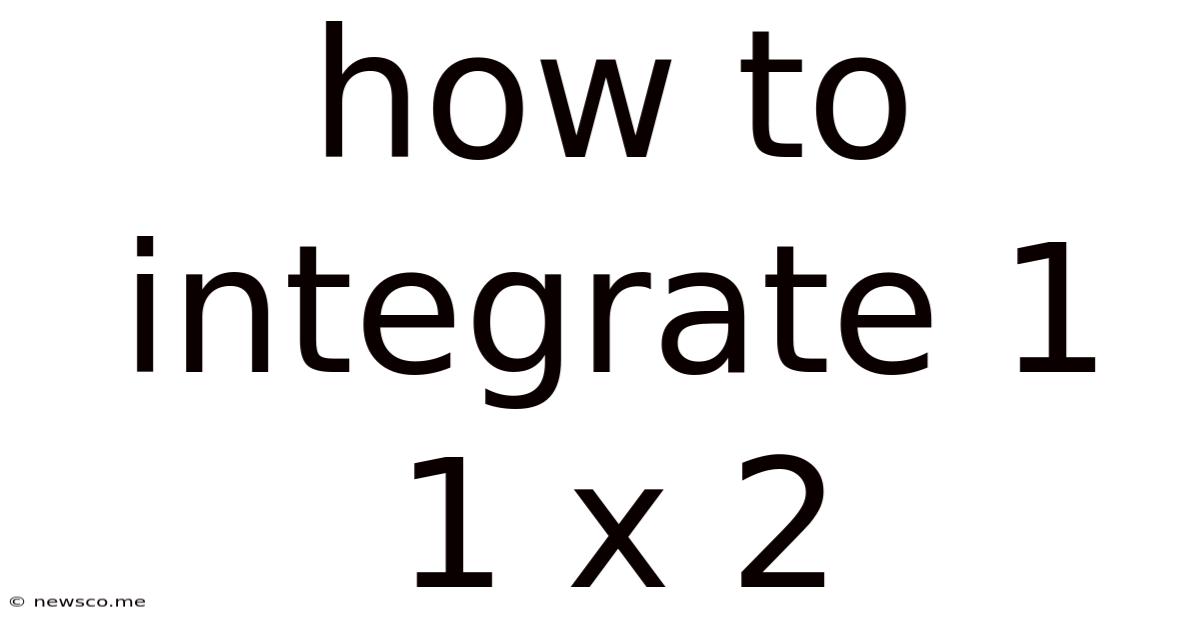
Table of Contents
How to Integrate 1/(1+x²) - A Comprehensive Guide
The integral of 1/(1+x²) is a fundamental concept in calculus with widespread applications in various fields. This comprehensive guide will walk you through different methods of solving this integral, explain its significance, and explore its practical uses. We'll cover both the direct integration method and delve into the underlying trigonometric substitution, ensuring a thorough understanding for all levels of mathematical expertise.
Understanding the Integral
Before we dive into the solution, let's clarify what we're aiming to achieve. The expression ∫ 1/(1+x²) dx represents the indefinite integral of the function f(x) = 1/(1+x²). This means we're searching for a function F(x) whose derivative, F'(x), is equal to 1/(1+x²).
Method 1: Direct Integration using the Arctangent Function
The most straightforward way to solve this integral is by recognizing it as a standard integral directly related to the inverse tangent function (arctangent).
The key is to remember this crucial identity:
∫ 1/(1+x²) dx = arctan(x) + C
where 'C' represents the constant of integration. This constant is crucial because the derivative of any constant is zero. Therefore, infinitely many functions can have the same derivative.
This method is concise and efficient. However, for a deeper understanding of why this is the solution, let's examine the trigonometric substitution method.
Method 2: Trigonometric Substitution
This method provides a more in-depth understanding of the integral's solution. We'll use a trigonometric substitution to transform the integrand into a simpler form that we can easily integrate.
1. The Substitution:
We make the substitution x = tan(θ). This implies that dx = sec²(θ) dθ.
2. Substituting into the Integral:
Replacing x and dx in the original integral, we get:
∫ 1/(1 + x²) dx = ∫ 1/(1 + tan²(θ)) * sec²(θ) dθ
3. Simplifying using Trigonometric Identities:
Recall the Pythagorean trigonometric identity: 1 + tan²(θ) = sec²(θ). Substituting this into the integral simplifies it significantly:
∫ 1/(1 + tan²(θ)) * sec²(θ) dθ = ∫ 1/sec²(θ) * sec²(θ) dθ = ∫ 1 dθ
4. Integrating:
The integral of 1 with respect to θ is simply θ:
∫ 1 dθ = θ + C
5. Back-Substitution:
Since we initially substituted x = tan(θ), we need to express θ in terms of x. Taking the inverse tangent of both sides, we get θ = arctan(x).
6. Final Result:
Substituting this back into our result, we obtain the same solution as before:
θ + C = arctan(x) + C
Therefore, we've proven through trigonometric substitution that:
∫ 1/(1 + x²) dx = arctan(x) + C
The Significance of the Arctangent Function
The arctangent function, denoted as arctan(x) or tan⁻¹(x), is the inverse function of the tangent function. It returns the angle whose tangent is x. This function plays a critical role in various mathematical and scientific applications.
-
Geometry: It's used to calculate angles in right-angled triangles, given the ratio of the opposite side to the adjacent side.
-
Physics: It appears in many physics equations, particularly in problems involving angles and vectors. For instance, it's used in calculating the trajectory of projectiles.
-
Engineering: The arctangent function finds applications in signal processing, control systems, and many other engineering disciplines.
-
Computer Graphics: It's essential in 3D graphics and game development for manipulating rotations and orientations.
Applications of the Integral ∫ 1/(1+x²) dx
The integral ∫ 1/(1+x²) dx = arctan(x) + C has extensive applications in various fields:
-
Probability and Statistics: It's integral to calculating probabilities related to the standard normal distribution. The probability density function of the standard normal distribution involves this integral.
-
Complex Analysis: This integral is fundamental in complex analysis, particularly in the evaluation of contour integrals and the calculation of residues.
-
Differential Equations: Solving certain types of differential equations often involves this integral as a step in the solution process.
-
Physics (again!): It appears in solutions for problems involving electric and magnetic fields, particularly those with radial symmetry. For example, calculating the electric potential due to a point charge involves this integral.
Definite Integrals and Applications
While we've focused on indefinite integrals, the definite integral of 1/(1+x²) is equally important. The definite integral is calculated as follows:
∫(from a to b) 1/(1+x²) dx = arctan(x) | (from a to b) = arctan(b) - arctan(a)
This provides a numerical value representing the area under the curve of 1/(1+x²) between the limits a and b. This has specific uses in:
-
Calculating probabilities: In probability, this helps calculate the probability of a random variable falling within a specific range.
-
Determining area: This helps in calculating the area of a region bounded by the curve y = 1/(1+x²), the x-axis, and vertical lines at x = a and x = b.
-
Physics (and again!): This helps to calculate physical quantities that depend on integration of this function over a defined interval.
Advanced Topics and Extensions
While this guide focuses on the basic integration, several advanced topics extend the concept:
-
Integration of similar functions: Understanding this integral provides the foundation for integrating other functions that can be manipulated to resemble the form 1/(1+x²).
-
Partial fraction decomposition: This technique can help decompose more complex rational functions into simpler fractions, some of which may include terms integrable using the arctangent function.
-
Numerical methods of integration: If the integral cannot be solved analytically, numerical techniques (like the trapezoidal rule or Simpson's rule) can provide approximate solutions.
Conclusion
The integral of 1/(1+x²) is a cornerstone concept in calculus, with profound significance and widespread applications across diverse fields. Understanding both the direct integration method and the trigonometric substitution method provides a solid foundation for tackling more complex integration problems. The arctangent function, central to the solution, plays a crucial role in various mathematical and scientific disciplines. This guide has aimed to provide a complete and comprehensive understanding of this fundamental integral, from its basic calculation to its advanced applications. Remember that consistent practice and exploration are key to mastering integration techniques.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Integrate 1 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.