How To Solve X 2 5
News Co
May 08, 2025 · 5 min read
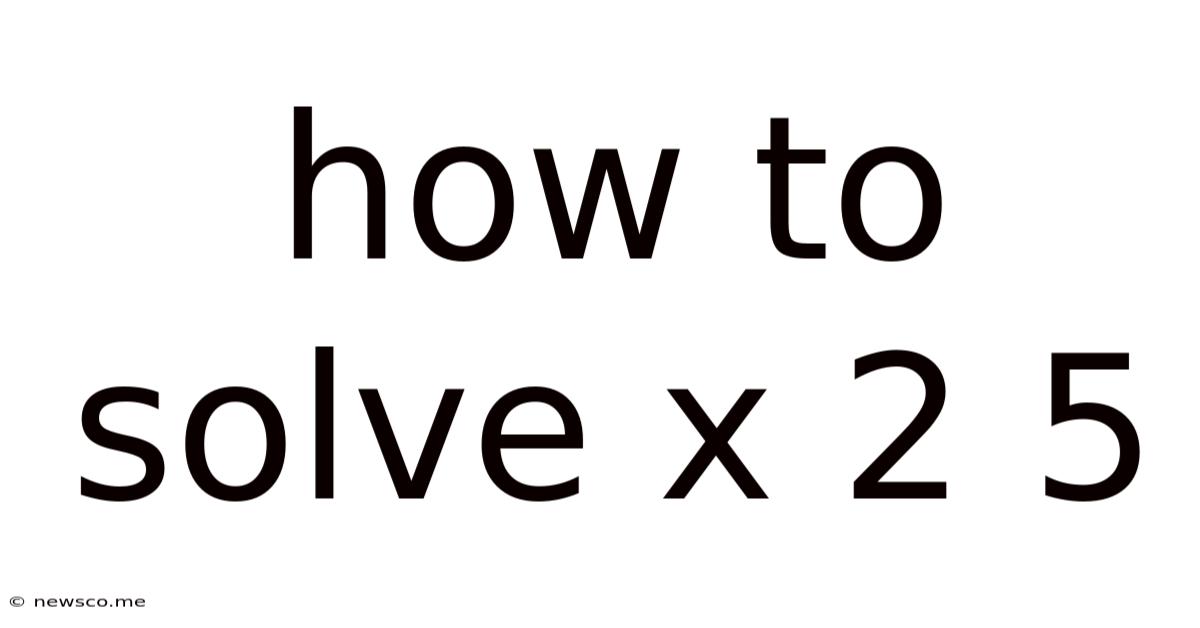
Table of Contents
How to Solve x² = 5: A Comprehensive Guide
Solving the equation x² = 5 might seem straightforward, but understanding the nuances and implications is crucial for a strong foundation in algebra. This comprehensive guide will delve into various methods to solve this equation, exploring both the conceptual understanding and the practical application. We'll cover different approaches, highlighting their strengths and weaknesses, and providing clear, step-by-step instructions. We'll also discuss the significance of understanding both the positive and negative solutions and the broader implications for solving quadratic equations.
Understanding the Problem: x² = 5
The equation x² = 5 asks us to find the value(s) of 'x' that, when squared (multiplied by itself), equal 5. This is a fundamental type of quadratic equation, meaning it involves the variable 'x' raised to the power of 2. The simplicity of the equation might be deceptive, as it introduces a key concept in algebra: the existence of multiple solutions.
Method 1: Using the Square Root Property
This is arguably the most direct and commonly used method. The square root property states that if x² = a, then x = ±√a. Applying this to our equation, x² = 5:
1. Take the Square Root of Both Sides:
√x² = ±√5
2. Simplify:
x = ±√5
This gives us two solutions:
- x = √5 (approximately 2.236)
- x = -√5 (approximately -2.236)
It's crucial to remember the ± (plus or minus) symbol. Squaring both positive and negative √5 will result in 5. Ignoring the negative solution is a common mistake and would lead to an incomplete answer.
Why the ± Symbol is Crucial
The significance of the ± symbol cannot be overstated. It directly relates to the fundamental theorem of algebra, which states that a polynomial of degree n has exactly n roots (solutions), possibly including complex numbers and repeated roots. In our case, x² = 5, a polynomial of degree 2, therefore has exactly two roots. Understanding this ensures a complete solution to the equation.
Method 2: Factoring (Not Directly Applicable, but Illustrative)
While direct factoring isn't the most efficient method for solving x² = 5, it's useful to consider for understanding broader quadratic equation-solving techniques. We can rewrite the equation as:
x² - 5 = 0
This equation represents a parabola that intersects the x-axis at two points. However, this specific quadratic equation doesn't factor nicely using integers. We'd need to resort to more advanced techniques, like the quadratic formula (discussed below), which inherently handles cases where factoring isn't easily apparent.
Method 3: The Quadratic Formula: A General Approach
The quadratic formula is a powerful tool for solving any quadratic equation of the form ax² + bx + c = 0. Our equation, x² = 5, can be rewritten as x² + 0x - 5 = 0, where a = 1, b = 0, and c = -5. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values:
x = [0 ± √(0² - 4 * 1 * -5)] / (2 * 1) x = ± √20 / 2 x = ± 2√5 / 2 x = ± √5
This again yields the same two solutions: x = √5 and x = -√5. The quadratic formula provides a robust method applicable to all quadratic equations, even those that don't factor easily.
Understanding the Discriminant (b² - 4ac)
The expression b² - 4ac inside the square root in the quadratic formula is known as the discriminant. It determines the nature of the solutions:
- b² - 4ac > 0: Two distinct real solutions (as in our case)
- b² - 4ac = 0: One real solution (a repeated root)
- b² - 4ac < 0: Two complex solutions (involving imaginary numbers)
In our equation, the discriminant is 20, indicating two distinct real solutions.
Method 4: Graphical Representation
A visual approach can enhance understanding. Graphing the equation y = x² and y = 5 reveals the points of intersection, representing the solutions. The parabola y = x² intersects the horizontal line y = 5 at two points, reflecting the two solutions, x = √5 and x = -√5. This visual representation provides a geometric interpretation of the algebraic solution.
Approximating √5
Since √5 is an irrational number (it cannot be expressed as a simple fraction), its decimal representation is non-terminating and non-repeating. However, we can approximate its value using various methods:
- Calculator: The most straightforward method is using a calculator to find the approximate value (approximately 2.236).
- Babylonian Method (or Heron's Method): This iterative method refines an initial guess to approach the square root. It's a historically significant method that illustrates numerical approximation techniques.
- Long Division Method: While less efficient, this method demonstrates a manual approach to calculating square roots, highlighting the underlying mathematical principles.
Applications and Further Exploration
Solving equations like x² = 5 is fundamental to many areas of mathematics and science:
- Geometry: Calculating lengths, areas, and volumes often involve solving quadratic equations.
- Physics: Describing projectile motion, oscillations, and many other phenomena require solving quadratic equations.
- Engineering: Designing structures, analyzing circuits, and numerous other engineering tasks rely on solving quadratic and other higher-order equations.
- Calculus: Finding roots of functions is crucial in calculus, and many techniques involve solving quadratic equations as intermediate steps.
Conclusion
Solving x² = 5, while seemingly simple, provides a crucial stepping stone to understanding quadratic equations and more advanced mathematical concepts. Mastering various solution methods, including the square root property, the quadratic formula, and graphical representation, is essential for success in algebra and related fields. Remember the importance of the ± symbol, understanding the discriminant, and appreciating the practical applications of this fundamental mathematical concept. The seemingly straightforward solution encapsulates key mathematical principles with far-reaching implications. Further exploration into numerical methods for approximating irrational solutions, such as √5, can significantly enhance one’s understanding and problem-solving skills in mathematics and beyond.
Latest Posts
Related Post
Thank you for visiting our website which covers about How To Solve X 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.