If 2/3 Of N Is 4
News Co
Mar 27, 2025 · 5 min read
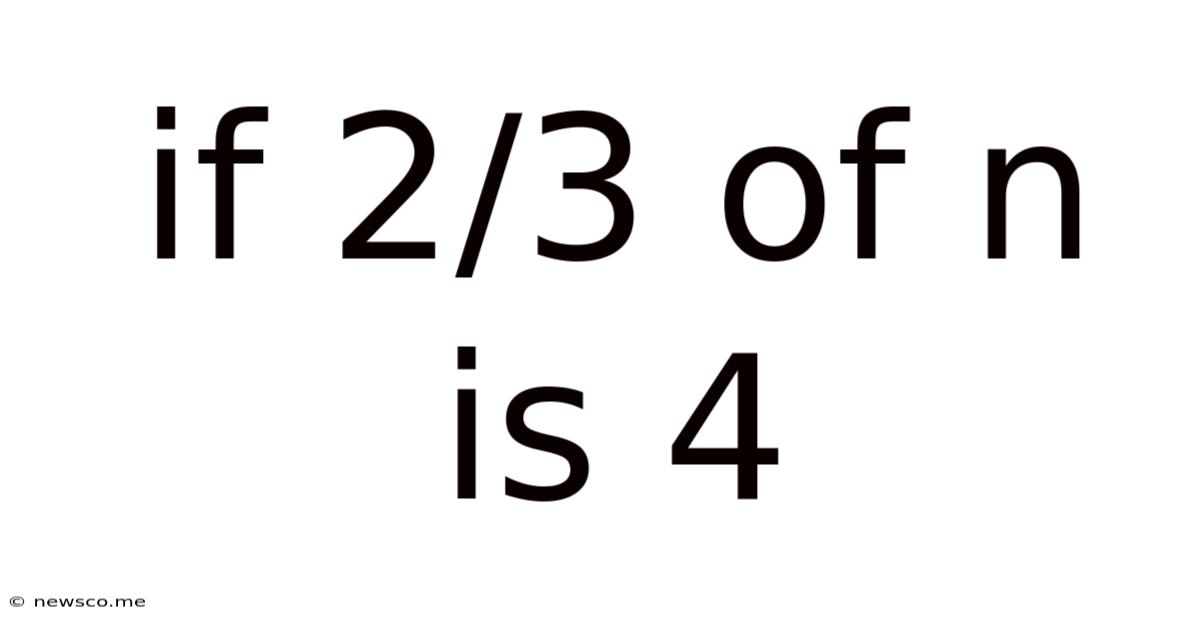
Table of Contents
If 2/3 of n is 4: A Deep Dive into Solving Proportions and Applications
This seemingly simple equation, "2/3 of n is 4," opens a door to a world of mathematical concepts, problem-solving strategies, and real-world applications. While the solution itself is straightforward, understanding the underlying principles and exploring its various interpretations provides a valuable learning experience. This article will delve into solving this equation, explore related mathematical concepts like proportions and ratios, and examine its applications in various fields.
Understanding the Problem: 2/3 of n = 4
The statement "2/3 of n is 4" translates directly into the algebraic equation:
(2/3)n = 4
This equation represents a proportion, a statement of equality between two ratios. Understanding proportions is crucial for solving this and similar problems. A ratio is a comparison of two quantities, while a proportion is an equation that states two ratios are equal. In this case, the ratio 2/3 is compared to the ratio 4/n.
Solving for n: A Step-by-Step Approach
Several methods can be used to solve for 'n'. Let's explore two common approaches:
Method 1: Multiplying by the Reciprocal
The most efficient way to solve for 'n' is to multiply both sides of the equation by the reciprocal of 2/3, which is 3/2. This cancels out the fraction on the left side:
(3/2) * (2/3)n = 4 * (3/2)
This simplifies to:
n = 12/2
Therefore:
n = 6
Method 2: Clearing the Fraction
Another approach involves clearing the fraction by multiplying both sides of the equation by the denominator (3):
3 * (2/3)n = 4 * 3
This simplifies to:
2n = 12
Then, divide both sides by 2:
n = 12/2
Therefore:
n = 6
Beyond the Solution: Exploring Proportions and Ratios
The equation "2/3 of n is 4" highlights the importance of understanding proportions and ratios in mathematics. Let's delve deeper into these concepts:
What are Ratios?
A ratio is a comparison of two quantities. It can be expressed in several ways:
- Using the colon: 2:3
- Using the word "to": 2 to 3
- Using a fraction: 2/3
Ratios are used to represent relationships between different quantities, such as the ratio of boys to girls in a class, the ratio of ingredients in a recipe, or the ratio of wins to losses in a sports season.
What are Proportions?
A proportion is an equation stating that two ratios are equal. The equation (2/3)n = 4 is a proportion. Proportions are used extensively in various applications, including scaling drawings, calculating percentages, and solving problems involving similar triangles. The fundamental property of proportions is that the cross-products are equal. In the given proportion:
(2/3) = (4/n)
The cross-products are:
2 * n = 3 * 4
This leads to the same equation we solved earlier:
2n = 12
Real-World Applications: Where Proportions Matter
Understanding and solving proportions is crucial in many real-world situations. Here are a few examples:
1. Scaling Recipes:
Imagine you have a recipe that yields 6 servings and you only want to make 4 servings. If the recipe calls for 2 cups of flour for 6 servings, you can use proportions to determine the amount of flour needed for 4 servings:
(2 cups / 6 servings) = (x cups / 4 servings)
Solving for x, we find that you'll need 4/3 cups of flour, or approximately 1.33 cups.
2. Map Scaling:
Maps use proportions to represent large geographical areas on a smaller scale. If a map has a scale of 1 inch representing 10 miles, and the distance between two cities on the map is 3 inches, the actual distance between those cities is:
(1 inch / 10 miles) = (3 inches / x miles)
Solving for x, the actual distance is 30 miles.
3. Percentage Calculations:
Percentages are essentially ratios expressed as a fraction of 100. For example, if 2/3 of students in a class passed an exam, and there were 6 students in the class, we can calculate the number of students who passed using proportions:
(2/3) = (x / 6)
Solving for x, we find that 4 students passed the exam (this also illustrates the original problem).
4. Financial Calculations:
Proportions are fundamental to many financial calculations, such as calculating interest, determining investment returns, and understanding financial ratios like debt-to-equity ratios. Understanding proportions allows for accurate assessment of financial health and performance.
5. Engineering and Construction:
In engineering and construction, proportions are used to scale blueprints, calculate material quantities, and ensure structural integrity. Precise proportions are critical for building accurate and safe structures.
6. Science and Research:
Many scientific experiments and research studies involve collecting and analyzing data using ratios and proportions. For instance, determining the concentration of a solution or calculating reaction rates often involves proportional relationships.
Expanding the Concepts: Further Exploration
The simple equation (2/3)n = 4 provides a springboard for exploring more complex mathematical concepts:
1. Solving More Complex Proportions:
We can extend this principle to solve more complex proportions with multiple variables. For example:
(a/b) = (c/d)
2. Understanding Ratios and Rates:
While related, ratios and rates have subtle differences. A rate is a ratio that compares two quantities with different units, such as speed (miles per hour) or density (grams per cubic centimeter).
3. Direct and Inverse Proportions:
Proportions can be either direct or inverse. In a direct proportion, as one quantity increases, the other increases proportionally. In an inverse proportion, as one quantity increases, the other decreases proportionally.
4. Applications in Geometry and Trigonometry:
Proportions play a significant role in geometry and trigonometry, especially when dealing with similar triangles and solving for unknown sides or angles.
Conclusion: The Power of Proportions
The seemingly simple equation "2/3 of n is 4" is a powerful illustration of the importance of understanding proportions and ratios. Solving this equation is straightforward, but exploring the underlying mathematical concepts and examining its diverse applications reveals its significance in various fields. Mastering proportions is a fundamental skill that empowers individuals to solve problems, understand data, and tackle real-world challenges effectively. From scaling recipes to designing bridges, the ability to work with proportions is a valuable asset in a wide range of disciplines. The journey from solving a simple equation to understanding its broad applications underscores the beauty and power of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about If 2/3 Of N Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.